Prezentācijas apraksts atsevišķos slaidos:

1 slaids

Slaida apraksts:

Nodarbības tēma: Atvasinājuma pielietošana dažādās zināšanu jomās Matemātikas skolotājs MBOU "Skola Nr. 74" Zagumennova Marina Vladimirovna

2 slaids

Slaida apraksts:

Nodarbības mērķis: Apgūt galvenās atvasinājuma pielietošanas jomas dažādās zinātnes un tehnikas jomās; Izmantojot praktisku problēmu risināšanas piemērus, apsveriet, kā atvasinājums tiek izmantots ķīmijā, fizikā, bioloģijā, ģeogrāfijā un ekonomikā.

3 slaids

Slaida apraksts:

"Nav nevienas matemātikas jomas, lai cik abstrakta tā būtu, kas kādreiz nebūtu piemērojama reālās pasaules parādībām." N.I. Lobačevskis

4 slaids

Slaida apraksts:

Diferenciācijas noteikumi Summas atvasinājums Par konstantu faktoru Produkta atvasinājums Daļas atvasinājums Sarežģītas funkcijas atvasinājums (u+v)"= u" + v' (Cu)"=Cu' (uv)"=u"v +uv' (u/v)" =(u"v-uv")/v2 hꞌ(x)=gꞌ(f(x))f ꞌ(x)

5 slaids

Slaida apraksts:

Atvasinājums fizikā Problēma. Automašīnas kustību bremzēšanas laikā apraksta ar formulu s(t) = 30t - 5t2, (s ir bremzēšanas ceļš metros, t ir laiks sekundēs no bremzēšanas sākuma līdz pilnīgai automašīnas apstāšanās brīdim). Atrodiet, cik sekundes automašīna ir kustībā no brīža, kad tā sāk bremzēt, līdz tā pilnībā apstājas. Kāds ir automašīnas nobrauktais attālums no bremzēšanas sākuma līdz pilnīgai apstāšanās brīdim? Risinājums: Tā kā ātrums ir pirmais kustības atvasinājums laikā, tad v = S'(t) = 30 - 10t, jo bremzējot ātrums nulle, tad 0=30–10t; 10t=30; t=3(s). Apstāšanās ceļš S(t) = 30t - 5t2 = 30∙3-5∙32 = 90-45 = 45(m). Atbilde: palēninājuma laiks 3s, bremzēšanas ceļš 45m.

6 slaids

Slaida apraksts:

Šis ir interesants Tvaikonis "Čeļuskins" 1934. gada februārī veiksmīgi izbrauca visu ziemeļu jūras ceļu, bet Beringa šaurums bija iesprostoti ledū. Ledus aiznesa Čeļuskinu uz ziemeļiem un saspieda to. Lūk, katastrofas apraksts: “Korpusa stiprais metāls nepadevās uzreiz,” radio ziņoja ekspedīcijas vadītājs O.Ju. Šmits. - Bija redzams, kā ledus gabals tika iespiests sānos un kā apvalka loksnes virs tā izspiedās, izliecoties uz āru. Ledus turpināja savu lēno, bet neatvairāmo virzību. Korpusa apšuvuma uzbriedušās dzelzs loksnes bija ieplīsušas pie šuves. Kniedes lidoja ar plaisu. Vienā mirklī kuģa borta borts tika norauts no priekšgala tilpnes līdz klāja pakaļgalam ... ”Kāpēc notika katastrofa?

7 slaids

Slaida apraksts:

Ledus spiediena spēks Р sadalās divās daļās: F un R. R ir perpendikulārs dēlim, F ir vērsts tangenciāli. Leņķis starp P un R - α - sānu leņķis pret vertikāli. Q ir ledus berzes spēks pret dēli. Q = 0,2 R (0,2 ir berzes koeficients). Ja Q< F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q >F, tad berze neļauj ledus gabalam slīdēt, un ledus var sasmalcināt un nospiest dēli. 0,2R< R tgα , tgα >0,2; J< F, если α >1100. Kuģa bortu slīpums pret vertikāli leņķī α > 1100 nodrošina drošu kuģošanu ledū.

8 slaids

Slaida apraksts:

Atvasinājums ķīmijā Ātruma noteikšanai izmanto atvasinājumu ķīmijā ķīmiskā reakcija. Tas nepieciešams: procesu inženieriem ķīmiskās ražošanas efektivitātes noteikšanā, ķīmiķiem, kas izstrādā zāles medicīnai un Lauksaimniecība, kā arī ārstiem un agronomiem, kuri lieto šīs zāles, lai ārstētu cilvēkus un lietotu tos augsnē. Lai atrisinātu ražošanas problēmas medicīnas, lauksaimniecības un ķīmiskajā rūpniecībā, vienkārši ir jāzina ķīmisko vielu reakcijas ātrums.

9 slaids

Slaida apraksts:

Ķīmijas uzdevums. Ķīmiskajā reakcijā nonākušās vielas daudzumu izsaka ar atkarību: р(t) = t2/2 + 3t –3 (mol). Atrodiet ķīmiskās reakcijas ātrumu pēc 3 sekundēm. Atsauce: Ķīmiskās reakcijas ātrums ir reaģentu koncentrācijas izmaiņas laika vienībā vai reaģentu koncentrācijas atvasinājums attiecībā pret laiku (matemātikas valodā koncentrācija būtu funkcija, un laiks būtu arguments )

10 slaids

Slaida apraksts:

Risinājums Jēdziens ķīmijas valodā Apzīmējums Jēdziens matemātikas valodā Vielas daudzums brīdī t0 p = p(t0) Funkcija Laika intervāls ∆t = t – t0 Argumenta pieaugums Vielas daudzuma izmaiņas ∆p = p(t0+ ∆ t) – p(t0) Funkcijas pieaugums Vidējais ķīmiskās reakcijas ātrums ∆p/∆t Funkcijas pieauguma attiecība pret argumenta pieaugumu V (t) = p'(t)

11 slaids

Slaida apraksts:

Atvasinājums bioloģijā Problēma bioloģijā: Pamatojoties uz zināmo populācijas lieluma x(t) atkarību, nosaka relatīvo pieaugumu laikā t. Atsauce: Populācija ir noteiktas sugas indivīdu kopums, kas aizņem noteiktu teritorijas apgabalu sugas areāla ietvaros, brīvi krustojas savā starpā un ir daļēji vai pilnībā izolēts no citām populācijām, kā arī ir elementāra vienība. par evolūciju.

12 slaids

Slaida apraksts:

Risinājums Jēdziens bioloģijas valodā Apzīmējums Jēdziens matemātikas valodā Iedzīvotāju skaits brīdī t x = x(t) Funkcija Laika intervāls ∆t = t – t0 Argumenta pieaugums Populācijas izmaiņas ∆x = x(t) – x(t0) Pieaugums funkcijas Izmaiņu ātrums populācijas lielums ∆x/∆t Funkcijas pieauguma attiecība pret argumenta pieaugumu Relatīvais pieaugums dotajā brīdī lim∆x/∆t ∆t → 0 Atvasinājums Р = x" (t)

13 slaids

Slaida apraksts:

14 slaids

Slaida apraksts:

Atvasinājums ģeogrāfijā Atvasinājums palīdz aprēķināt: Dažas vērtības seismogrāfijā Funkcijas elektromagnētiskais lauks Zeme Kodolģeofizikālo rādītāju radioaktivitāte Daudzas vērtības ekonomiskajā ģeogrāfijā Atvasiniet formulu, lai aprēķinātu iedzīvotāju skaitu teritorijā laikā t.

15 slaids

Slaida apraksts:

Ģeogrāfijas uzdevums Atvasināt formulu iedzīvotāju skaita aprēķināšanai ierobežotā teritorijā laikā t.

16 slaids

Slaida apraksts:

Risinājums Lai y=y(t) ir populācija. Aplūkosim iedzīvotāju skaita pieaugumu pie ∆t = t – t0 ∆у = k∙y∙∆t, kur k = kр – kс ir iedzīvotāju skaita pieauguma temps, (kр ir dzimstība, kс ir mirstība). ∆у/∆t = k∙y kā ∆t → 0 iegūstam lim ∆у/∆t = у’. Iedzīvotāju skaita pieaugums - y’ = k∙y. ∆t → 0 Secinājums: atvasinājums ģeogrāfijā ir apvienots ar daudzām tā nozarēm (seismogrāfija, atrašanās vieta un populācija), kā arī ar ekonomisko ģeogrāfiju. Tas viss ļauj pilnīgāk izpētīt pasaules iedzīvotāju un valstu attīstību.

17 slaids

Slaida apraksts:

Atvasinājums ekonomikā Atvasinātais risina svarīgus jautājumus: Kādā virzienā mainīsies valdības ienākumi, palielinoties nodokļiem vai ieviešot muitas nodevas? Vai uzņēmuma ieņēmumi palielināsies vai samazināsies, palielinoties tā produktu cenai? Lai atrisinātu šos jautājumus, ir jākonstruē ievades mainīgo savienojuma funkcijas, kuras pēc tam tiek pētītas ar diferenciālrēķina metodēm. Tāpat, izmantojot funkcijas ekstrēmu ekonomikā, var atrast augstāko darba ražīgumu, maksimālo peļņu, maksimālo izlaidi un minimālās izmaksas.

18 slaids

Slaida apraksts:

Problēma ekonomikā Nr.1 ​​(ražošanas izmaksas) Lai y ir ražošanas izmaksas, un x ir produkcijas daudzums, tad x1 ir ražošanas pieaugums, un y1 ir ražošanas izmaksu pieaugums.

19 slaids

Slaida apraksts:

20 slaids

Prezentācija par tēmu: "Atvasinājuma izmantošana zinātnē un dzīvē" Izpilda Phi-17 grupas audzēkne Dolženkova Anastasija Informācija no atvasinājuma parādīšanās vēstures: Daudzu XVII gadsimta matemātiķu sauklis. bija: "Ejiet uz priekšu, un ticība rezultātu pareizībai nāks pie jums." Terminu "atvasinājums" (franču atvasinājums - aiz, aiz) 1797. gadā ieviesa Dž.Lagranžs. Viņš arī ieviesa mūsdienu apzīmējumus y" , f'. apzīmējums lim ir saīsinājums no latīņu vārda limes (robeža, robeža). Terminu "robeža" ieviesa I. Ņūtons. I.Ņūtons atvasinājumu sauca par plūsmu, bet pašu funkciju - par plūstošu. G. Leibnics runāja par diferenciālo attiecību un apzīmēja atvasinājumu šādi: Lagranžs Džozefs Luiss (1736-1813) franču matemātiķis un mehāniķis Ņūtons:

“Šī pasaule bija dziļā tumsā. Lai top gaisma! Un šeit nāk Ņūtons. A. Pogue.

Īzaks Ņūtons (1643-1727) viens no diferenciālrēķinu radītājiem.

Viņa galvenajam darbam Dabas filozofijas matemātiskie principi bija milzīga ietekme uz dabaszinātņu attīstību un kļuva par pagrieziena punktu dabaszinātņu vēsturē.

Ņūtons ieviesa atvasinājuma jēdzienu, pētot mehānikas likumus, tādējādi atklājot tā mehānisko nozīmi.

Kas ir funkcijas atvasinājums?

Funkcijas atvasinājums noteiktā punktā ir funkcijas pieauguma attiecības robeža šajā punktā pret argumenta pieaugumu, ja argumenta pieaugumam ir tendence uz nulli.

Atvasinājuma fiziskā nozīme.

• Ātrums ir attāluma atvasinājums attiecībā pret laiku:
v(t) = S′(t)

• Paātrinājums ir ātruma atvasinājums attiecībā pret laiku:

a(t) = v′(t) = S′′(t)

Atvasinājuma ģeometriskā nozīme: Funkcijas grafika pieskares slīpums ir vienāds ar šīs funkcijas atvasinājumu, kas aprēķināts saskares punktā. f′(x) = k = tga Elektrotehnikas atvasinājums:

Mūsu mājās, transportā, rūpnīcās: elektriskā strāva darbojas visur. Zem elektriskās strāvas saprot brīvu elektriski lādētu daļiņu virzītu kustību.

Elektriskās strāvas kvantitatīvā īpašība ir strāvas stiprums.

Elektriskās strāvas ķēdē elektriskais lādiņš laika gaitā mainās atbilstoši q=q (t) likumam. Strāva I ir lādiņa q atvasinājums attiecībā pret laiku.

Elektrotehnikā galvenokārt tiek izmantots darbs maiņstrāva.

Elektrisko strāvu, kas mainās laika gaitā, sauc par maiņstrāvu. Maiņstrāvas ķēdē var būt dažādi elementi: sildītāji, spoles, kondensatori.

Maiņstrāvas iegūšana ir balstīta uz likumu elektromagnētiskā indukcija, kura sastāvs satur magnētiskās plūsmas atvasinājumu.

Atvasinājums ķīmijā:

• Un ķīmijā diferenciālrēķini ir atraduši plašu pielietojumu ķīmisko reakciju matemātisko modeļu konstruēšanā un turpmākajā to īpašību aprakstā.
• Ķīmija ir zinātne par vielām, vielu ķīmiskajām pārvērtībām.
• Ķīmija pēta dažādu reakciju modeļus.
• Ķīmiskās reakcijas ātrums ir reaģentu koncentrācijas izmaiņas laika vienībā.
• Tā kā reakcijas ātrums v procesa laikā nepārtraukti mainās, to parasti izsaka kā atvasinājums reaģentu koncentrācija laika gaitā.

Atvasinājums ģeogrāfijā:

Tomasa Maltusa socioloģiskā modeļa ideja ir tāda, ka iedzīvotāju skaita pieaugums ir proporcionāls iedzīvotāju skaitam noteiktā laikā t līdz N(t), . Maltusa modelis labi darbojās, lai aprakstītu ASV iedzīvotāju skaitu no 1790. līdz 1860. gadam. Šis modelis vairs nav derīgs lielākajā daļā valstu.

Integrālis un tā pielietojums: mazliet vēstures: Integrāļa jēdziena vēsture aizsākās matemātiķiem Senā Grieķija un Senā Roma. Zināmi ir Senās Grieķijas zinātnieka - Eudoksa no Knidosa (ap 408-ap 355 BC) darbi par ķermeņu tilpumu atrašanu un plakano figūru laukumu aprēķināšanu. Integrālie aprēķini kļuva plaši izplatīti 17. gadsimtā. Zinātnieki: G. Leibnics (1646-1716) un I. Ņūtons (1643-1727) neatkarīgi viens no otra un gandrīz vienlaikus atklāja formulu, kas vēlāk tika saukta par Ņūtona-Leibnica formulu, kuru mēs izmantojam. Tas, ka filozofs un fiziķis izdomāja matemātisko formulu, nevienu nepārsteidz, jo matemātika ir valoda, kurā runā pati daba. Integrālie aprēķini kļuva plaši izplatīti 17. gadsimtā. Zinātnieki: G. Leibnics (1646-1716) un I. Ņūtons (1643-1727) neatkarīgi viens no otra un gandrīz vienlaikus atklāja formulu, kas vēlāk tika saukta par Ņūtona-Leibnica formulu, kuru mēs izmantojam. Tas, ka filozofs un fiziķis izdomāja matemātisko formulu, nevienu nepārsteidz, jo matemātika ir valoda, kurā runā pati daba. Ievadīts simbols Ievadīts simbols Leibnics (1675). Šī zīme ir latīņu burta S variācija (vārda summa pirmais burts). Pats vārds neatņemama izgudrots J. Bernulli (1690). Tas, iespējams, nāk no latīņu integero, kas tulkojumā nozīmē atjaunot iepriekšējo stāvokli, atjaunot. Integrācijas robežas norādīja jau L. Eilers (1707-1783). 1697. gadā parādījās jaunas matemātikas nozares nosaukums - integrālrēķins. To ieviesa Bernulli. Matemātiskajā analīzē funkcijas integrālis ir summas jēdziena paplašinājums. Integrāļa atrašanas procesu sauc par integrāciju. Šo procesu parasti izmanto, meklējot tādus lielumus kā laukums, tilpums, masa, pārvietojums utt., kad tiek norādīts šī daudzuma izmaiņu ātrums vai sadalījums attiecībā pret kādu citu lielumu (pozīcija, laiks utt.). Kas ir integrālis? Integrālis ir viens no svarīgākajiem jēdzieniem matemātiskā analīze , kas rodas, risinot problēmas atrast laukumu zem līknes, nobraukto attālumu nevienmērīgas kustības laikā, neviendabīga ķermeņa masu utt., kā arī atjaunošanas uzdevumā. funkcijas pēc viņas teiktā atvasinājums Zinātnieki cenšas visas fizikālās parādības izteikt matemātiskas formulas veidā. Kad mums ir formula, mēs varam to izmantot, lai aprēķinātu jebko. Un integrālis ir viens no galvenajiem rīkiem darbam ar funkcijām. Zinātnieki cenšas visas fizikālās parādības izteikt matemātiskas formulas veidā. Kad mums ir formula, mēs varam to izmantot, lai aprēķinātu jebko. Un integrālis ir viens no galvenajiem rīkiem darbam ar funkcijām. Integrācijas metodes:

• Tabulas.
• Integranda pārveidošana par tabulu par summu vai starpību.
• Integrācija ar mainīgā lieluma maiņu (aizvietošana).
• Integrācija pa daļām.

Integrāļa pielietojums:

• Matemātika
• S figūru aprēķini.
• Līknes loka garums.
• V ķermeņi S paralēlos posmos.
• V revolūcijas ķermeņi utt.

• Fizika
• Darbs Mainīgs spēks.
• S - kustības ceļš.
• Masas aprēķins.
• Taisnes, riņķa, cilindra inerces momenta aprēķins.
• Smaguma centra koordinātu aprēķins.
• Siltuma daudzums utt.

Saratovas apgabala Izglītības ministrija

Valsts autonomais profesionālis izglītības iestāde Saratovas apgabals "Engelsas politehnikums"

ATVASINĀJUMA PIELIETOJUMS DAŽĀDĀS ZINĀTNES JOMĀS

Izpildīts: Sarkulova Nurgulja Sergejevna

KShI-216/15 grupas audzēknis

(Dizains, modelēšana un

šūšanas tehnoloģija)

Zinātniskais padomnieks:

Verbitskaja Jeļena Vjačeslavovna

matemātikas skolotājs GAPOU SO

"Eņģeļa politehnikums"

2016

Ievads

Matemātikas loma dažādās dabaszinātņu jomās ir ļoti liela. Nav brīnums, ka viņi saka“Matemātika ir zinātņu karaliene, tās fizika labā roka, ķīmija ir atstāta.

Pētījuma priekšmets ir atvasinājums.

Vadošais mērķis ir parādīt atvasinājuma nozīmi ne tikai matemātikā, bet arī citās zinātnēs, tā nozīmi mūsdienu dzīvē.

Diferenciālrēķins ir apkārtējās pasaules apraksts, kas veidots matemātiskā valodā. Atvasinājums palīdz mums veiksmīgi atrisināt ne tikai matemātikas uzdevumi, bet arī praktiski uzdevumi dažādās zinātnes un tehnikas jomās.

Funkcijas atvasinājumu izmanto visur, kur notiek nevienmērīga procesa plūsma: tā ir nevienmērīga mehāniskā kustība un maiņstrāva, un ķīmiskās reakcijas un vielas radioaktīvā sabrukšana utt.

Šīs esejas galvenie un tematiskie jautājumi:

1. Atvasinājuma rašanās vēsture.

2. Kāpēc pētīt funkciju atvasinājumus?

3. Kur tiek izmantoti atvasinājumi?

4. Atvasinājumu pielietojums fizikā, ķīmijā, bioloģijā un citās zinātnēs.

5. Secinājumi

Nolēmu uzrakstīt referātu par tēmu "Atvasinājuma pielietojums dažādās zinātnes jomās", jo šī tēma, manuprāt, ir ļoti interesanta, noderīga un aktuāla.

Savā darbā es runāšu par diferenciācijas pielietojumu dažādās zinātnes jomās, piemēram, ķīmijā, fizikā, bioloģijā, ģeogrāfijā uc Galu galā visas zinātnes ir nesaraujami saistītas, kas ļoti skaidri redzams tēmas piemērā. es apsveru.

Atvasinājuma pielietojums dažādās zinātnes jomās

No vidusskolas algebras kursa mēs to jau zinām atvasinājums ir funkcijas pieauguma un tās argumenta pieauguma attiecības robeža, jo argumenta pieaugumam ir tendence uz nulli, ja šāda robeža pastāv.

Atvasinājuma atrašanas darbību sauc par tā diferenciāciju, un funkciju, kurai ir atvasinājums punktā x, sauc par diferencējamu šajā punktā. Funkciju, kas ir diferencējama katrā intervāla punktā, sauc par diferencējamu šajā intervālā.

Gods atklāt matemātiskās analīzes pamatlikumus pieder angļu fiziķim un matemātiķim Īzakam Ņūtonam un vācu matemātiķim, fiziķim, filozofam Leibnicam.

Ņūtons ieviesa atvasinājuma jēdzienu, pētot mehānikas likumus, tādējādi atklājot tā mehānisko nozīmi.

Atvasinājuma fiziskā nozīme: funkcijas atvasinājumsy= f(x) punktā x 0 ir funkcijas izmaiņu ātrumsf(x) punktā x 0 .

Leibnics nonāca pie atvasinājuma jēdziena, atrisinot atvasinātās līnijas pieskares vilkšanas problēmu, tādējādi izskaidrojot tā ģeometrisko nozīmi.

Atvasinājuma ģeometriskā nozīme ir tāda, ka atvasinājuma funkcija punktāx 0 vienāds ar pieskares slīpumu funkcijas grafikam, kas novilkta punktā ar abscisux 0 .

Termins atvasinājums un mūsdienu apzīmējumsy" , f“Ieviesa Dž.Lagrenžs 1797. gadā.

19. gadsimta krievu matemātiķis Panfutijs Ļvovičs Čebiševs teica, ka "tās zinātnes metodes, kas ļauj atrisināt visiem kopīgu problēmu praktiskās aktivitātes cilvēks, piemēram, kā atbrīvoties no saviem līdzekļiem, lai sasniegtu vislielāko labumu.

Ar šādiem uzdevumiem mūsdienās jātiek galā dažādu specialitāšu pārstāvjiem:

Procesu inženieri cenšas organizēt ražošanu tā, lai tiktu saražots pēc iespējas vairāk produktu;

Dizaineri cenšas izstrādāt ierīci kosmosa kuģis tā, lai ierīces masa būtu mazākā;

Saiknes starp ražotni un izejvielu avotiem ekonomisti cenšas plānot tā, lai transportēšanas izmaksas būtu minimālas.

Studējot jebkuru tēmu, studentiem rodas jautājums: "Kāpēc mums tas ir vajadzīgs?" Ja atbilde apmierina ziņkāri, tad var runāt par skolēnu interesi. Atbildi par tēmu "Atvasinājums" var iegūt, zinot, kur tiek izmantoti funkciju atvasinājumi.

Lai atbildētu uz šo jautājumu, mēs varam uzskaitīt dažas disciplīnas un to sadaļas, kurās tiek izmantoti atvasinājumi.

Atvasinājums algebrā:

1. Funkcijas grafika pieskare

Funkcijas grafika pieskaresf, diferencējams ar x par , ir taisne, kas iet caur punktu (x par ; f(x o )) un kam ir slīpumsf'(x o ).

y= f(x o ) + f′(x o ) (x - x o )

2. Palielinošu un samazinošu funkciju intervālu meklēšana

Funkcijay=f(x) intervālā palielināsX , ja par kādu unnevienlīdzība. Citiem vārdiem sakot - lielāka vērtība arguments atbilst lielākajai funkcijas vērtībai.

Funkcijay=f(x) intervālā samazināsX , ja par kādu unnevienlīdzība. Citiem vārdiem sakot, lielāka argumenta vērtība atbilst mazākai funkcijas vērtībai.

3. Funkcijas galējo punktu atrašana

punktu saucamaksimālais punkts funkcijasy=f(x) ja par visiemx . Tiek izsaukta funkcijas vērtība maksimālajā punktāfunkcijas maksimums un apzīmē.

punktu saucaminimālais punkts funkcijasy=f(x) ja par visiemx no tās apkārtnes nevienlīdzību. Tiek izsaukta funkcijas vērtība minimālajā punktāfunkcijas minimums un apzīmē.

Zem punkta apkārtnes saprast intervālu, kur ir pietiekami mazs pozitīvs skaitlis.

Tiek izsaukti minimālie un maksimālie punktiekstremālie punkti , un tiek izsauktas funkciju vērtības, kas atbilst galējiem punktiemfunkciju ekstremitāte .

4. Funkcijas izliekuma un ieliekuma intervālu meklēšana

Funkciju grafiks, atrodas šajā intervālāizliekts , neatrodas augstāk par jebkuru no tā pieskarēm (1. att.).

Funkciju grafiks, diferencējams pēc intervāla, atrodas šajā intervālāieliekts , ja šīs funkcijas grafiks atrodas intervālā atrodas ne zemāk par kādu no tā pieskarēm (2. att.).

Funkcijas grafika lēciena punktu sauc par punktu, kas atdala izliekuma un ieliekuma intervālus.

5. Funkcijas lēciena punktu atrašana

Atvasinājums fizikā:

1. Ātrums kā ceļa atvasinājums

2. Paātrinājums kā ātruma atvasinājumsa =

3. Radioaktīvo elementu sabrukšanas ātrums 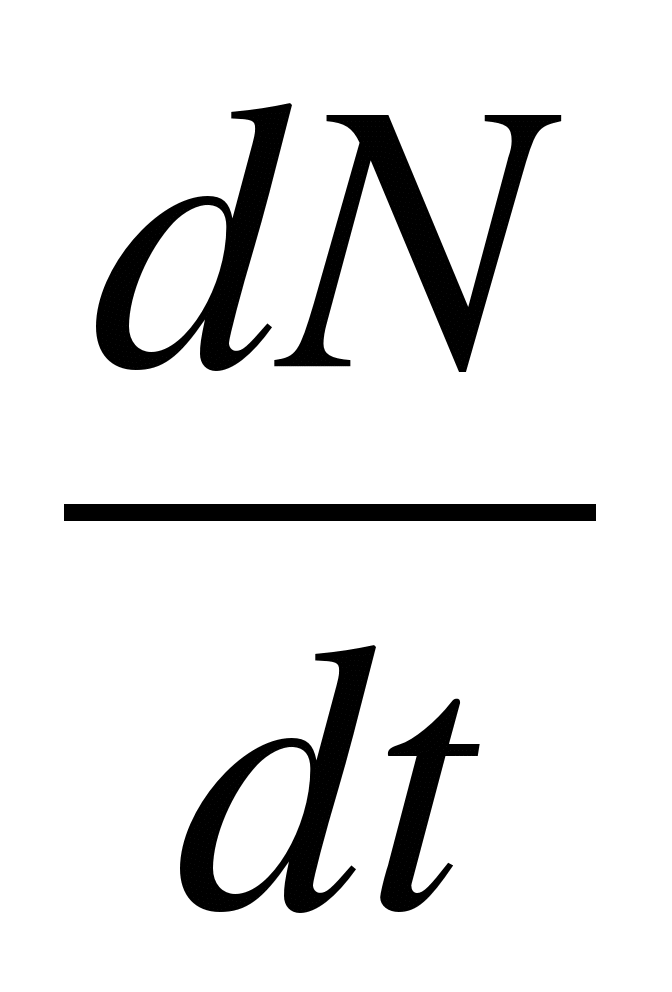= - λN

Un arī fizikā atvasinājumu izmanto, lai aprēķinātu:

Materiālu punktu ātrumi

Momentānais ātrums kā atvasinājuma fiziskā nozīme

Momentānā maiņstrāva

Elektromagnētiskās indukcijas EML momentānā vērtība

Maksimālā jauda

Atvasinājums ķīmijā:

Un ķīmijā diferenciālrēķini ir atraduši plašu pielietojumu ķīmisko reakciju matemātisko modeļu konstruēšanā un turpmākajā to īpašību aprakstā.

Atvasinājums ķīmijā tiek izmantots, lai noteiktu ļoti svarīgu lietu - ķīmiskās reakcijas ātrumu, vienu no izšķirošajiem faktoriem, kas jāņem vērā daudzās zinātniskās un rūpnieciskās darbības jomās.. V(t) = p'(t)

Daudzums

in-va laikā t 0

p = p(t 0 )

Funkcija

Laika intervāls

∆t = t–t 0

Argumentu pieaugums

Daudzuma maiņa

∆p=p(t 0 + ∆t) – p(t 0 )

Funkciju pieaugums

Vidējais ķīmiskās reakcijas ātrums

∆p/∆t

Funkcijas pieauguma attiecība pret argumentu pieaugumu

Atvasinājums bioloģijā:

Populācija ir noteiktas sugas indivīdu kopums, kas aizņem noteiktu teritorijas apgabalu sugas areāla ietvaros, brīvi krustojas savā starpā un ir daļēji vai pilnībā izolēts no citām populācijām, kā arī ir elementāra evolūcijas vienība. .

P \u003d x' (t)

Atvasinājums ģeogrāfijā:

1. Dažas nozīmes seismogrāfijā

2. Zemes elektromagnētiskā lauka īpatnības

3. Kodolģeofizikālo rādītāju radioaktivitāte

4. Daudzas nozīmes ekonomiskajā ģeogrāfijā

5. Atvasināt formulu iedzīvotāju skaita aprēķināšanai teritorijā laikā t.

y'= uz y

Tomasa Maltusa socioloģiskā modeļa ideja ir tāda, ka iedzīvotāju skaita pieaugums ir proporcionāls iedzīvotāju skaitam noteiktā laikā no t līdz N(t). Maltusa modelis darbojās labi, lai aprakstītu ASV iedzīvotāju skaitu no 1790. līdz 1860. gadam. Šis modelis vairs nav derīgs lielākajā daļā valstu.

Elektrotehnikas atvasinājums:

Mūsu mājās, transportā, rūpnīcās: elektriskā strāva darbojas visur. Zem elektriskās strāvas saprot brīvu elektriski lādētu daļiņu virzītu kustību.

Elektriskās strāvas kvantitatīvā īpašība ir strāvas stiprums.

Elektriskās strāvas ķēdē elektriskais lādiņš laika gaitā mainās atbilstoši q=q (t) likumam. Strāva I ir lādiņa q atvasinājums attiecībā pret laiku.

Elektrotehnikā galvenokārt tiek izmantota maiņstrāvas darbība.

Elektrisko strāvu, kas mainās laika gaitā, sauc par maiņstrāvu. Maiņstrāvas ķēdē var būt dažādi elementi: sildītāji, spoles, kondensatori.

Maiņstrāvas ražošanas pamatā ir elektromagnētiskās indukcijas likums, kura formulējums satur magnētiskās plūsmas atvasinājumu.

Atvasinājums ekonomikā:

Ekonomika ir dzīves pamats, un tajā nozīmīgu vietu ieņem diferenciālrēķini, ekonomiskās analīzes aparāts. Ekonomiskās analīzes pamatuzdevums ir izpētīt ekonomisko lielumu attiecības funkciju formā.

Atvasinājums ekonomikā atrisina svarīgus jautājumus:

1. Kādā virzienā mainīsies valsts ienākumi līdz ar nodokļu pieaugumu vai ar muitas nodevu ieviešanu?

2. Vai uzņēmuma ieņēmumi pieaugs vai samazināsies, palielinoties tā produkcijas cenai?

Lai atrisinātu šos jautājumus, ir jākonstruē ievades mainīgo savienojuma funkcijas, kuras pēc tam tiek pētītas ar diferenciālrēķina metodēm.

Tāpat, izmantojot funkcijas ekstrēmu (atvasinājumu) ekonomikā, var atrast augstāko darba ražīgumu, maksimālo peļņu, maksimālo izlaidi un minimālās izmaksas.

SECINĀJUMS: atvasinājums tiek veiksmīgi izmantots dažādu lietišķu problēmu risināšanā zinātnē, tehnoloģijā un dzīvē

Kā redzams no iepriekš minētā, funkcijas atvasinājuma lietojums ir ļoti daudzveidīgs un ne tikai matemātikas, bet arī citās disciplīnās. Līdz ar to varam secināt, ka tēmas "Funkcijas atvasinājums" izpētei būs pielietojums arī citās tēmās un priekšmetos.

Pārliecinājāmies par tēmas "Atvasinājums" izpētes nozīmi, lomu zinātnes un tehnikas procesu izpētē, iespēju projektēt atbilstoši reāli notikumi matemātiskos modeļus un atrisināt svarīgas problēmas.

“Mūzika var pacelt vai nomierināt dvēseli,
Glezniecība ir acij tīkama,
Dzeja - pamodināt jūtas,
Filozofija - apmierināt prāta vajadzības,
Inženierzinātnes ir uzlabot cilvēku dzīves materiālo pusi,
BETmatemātika var sasniegt visus šos mērķus.

Tā teica amerikāņu matemātiķisMoriss Klīns.

Bibliogrāfija:

1. Bogomolovs Ņ.V., Samojļenko I.I. Matemātika. - M.: Yurayt, 2015.

2. V. P. Grigorjevs un Ju. A. Dubinskis, Augstākās matemātikas elementi. - M.: Akadēmija, 2014.

3. Bavrins I.I. Augstākās matemātikas pamati. - M.: pabeigt skolu, 2013.

4. Bogomolovs Ņ.V. Semināri matemātika. - M.: Augstskola, 2013.

5. Bogomolovs Ņ.V. Matemātikas uzdevumu krājums. - M.: Bustard, 2013.

6. Ribņikovs K.A. Matemātikas vēsture, Maskavas universitātes apgāds, M, 1960.

7. Vinogradovs Yu.N., Gomola A.I., Potapovs V.I., Sokolova E.V. – M.:Izdevniecības centrs "Akadēmija", 2010.g

8 . Bašmakovs M.I. Matemātika: algebra un matemātiskās analīzes pirmsākumi, ģeometrija. - M.: Izdevniecības centrs "Akadēmija", 2016

Periodiskie avoti:

Laikraksti un žurnāli: "Matemātika", " Publiskā nodarbība»

Interneta resursu izmantošana, digitālās bibliotēkas:

www:egetutor.ru

matematika-na5.norod.ru

Atpakaļ uz priekšu

Uzmanību! Slaida priekšskatījums ir paredzēts tikai informatīviem nolūkiem, un tas var neatspoguļot visu prezentācijas apjomu. Ja jūs interesē šis darbs, lūdzu, lejupielādējiet pilno versiju.

Nodarbības veids: integrēta.

Nodarbības mērķis: izpētīt dažus atvasinājuma pielietojuma aspektus dažādās fizikas, ķīmijas, bioloģijas jomās.

Uzdevumi: skolēnu redzesloka paplašināšana un izziņas darbība, attīstība loģiskā domāšana un spēju pielietot savas zināšanas.

Tehniskā palīdzība: interaktīvā tāfele; dators un disks.

NODARBĪBU LAIKĀ

I. Organizatoriskais moments

II. Nodarbības mērķa noteikšana

- Es vēlētos vadīt nodarbību ar padomju matemātiķa un kuģu būvētāja Alekseja Nikolajeviča Krilova moto: "Teorija bez prakses ir mirusi vai bezjēdzīga, prakse bez teorijas ir neiespējama vai kaitīga."

Apskatīsim pamatjēdzienus un atbildēsim uz jautājumiem:

Kāda ir atvasinājuma pamatdefinīcija?
– Ko jūs zināt par atvasinājumu (īpašības, teorēmas)?
– Vai jūs zināt atvasinātu problēmu piemērus fizikā, matemātikā un bioloģijā?

Atvasinājuma pamatdefinīcijas izskatīšana un tās pamatojums (atbilde uz pirmo jautājumu):

Atvasinājums ir viens no matemātikas pamatjēdzieniem. Spējai risināt problēmas, izmantojot atvasinājumu, nepieciešamas labas zināšanas teorētiskais materiāls spēja veikt pētījumus dažādās situācijās.

Tāpēc šodien nodarbībā nostiprināsim un sistematizēsim iegūtās zināšanas, izskatīsim un izvērtēsim katras grupas darbu un, izmantojot dažu uzdevumu piemēru, parādīsim, kā izmantot atvasinājumu citu problēmu un nestandarta uzdevumu risināšanai, izmantojot atvasinājums.

III. Jaunā materiāla skaidrojums

1. Momentānā jauda ir darba atvasinājums attiecībā pret laiku:

W = lim ∆A/∆t ∆A – darba maiņa.

2. Ja ķermenis griežas ap asi, tad griešanās leņķis ir laika funkcija t
Tad leņķiskais ātrums ir:

W = lim Δφ/Δt = φ׳(t) Δ t → 0

3. Strāvas stiprums ir atvasinājums Ι = lim Δg/Δt = g′, kur g- pozitīvs elektriskais lādiņš, kas laikā pārnests caur vadītāja šķērsgriezumu Δt.

4. Ļaujiet ∆Q ir siltuma daudzums, kas nepieciešams, lai mainītu temperatūru Δt tad laiks lim ΔQ/Δt = Q′ = C –īpašs karstums.

5. Ķīmiskās reakcijas ātruma problēma

m(t) – m(t0) – vielas daudzums, kas laika gaitā reaģē t0 pirms tam t

V= lim ∆m/∆t = m ∆t → 0

6. Radioaktīvās vielas masa ir m. Radioaktīvās sabrukšanas ātrums: V = lim ∆m/∆t = m׳(t) ∆t→0

Diferencētā veidā radioaktīvās sabrukšanas likumam ir šāda forma: dN/dt = – λN, kur N ir to kodolu skaits, kas laika gaitā nav sabrukuši t.

Integrējot šo izteiksmi, mēs iegūstam: dN/N = – λdt ∫dN/N = – λ∫dt lnN = – λt + c, c = konst. plkst t = 0 radioaktīvo kodolu skaits N = N0, tāpēc mums ir: log N0 = konst., sekojoši

n N = – λt + ln N0.

Pastiprinot šo izteiksmi, mēs iegūstam:

ir radioaktīvās sabrukšanas likums, kur N0 ir kodolu skaits vienlaikus t0 = 0, N ir to kodolu skaits, kas laika gaitā nav sabrukuši t.

7. Saskaņā ar Ņūtona siltuma pārneses vienādojumu, siltuma plūsmas ātrums dQ/dt ir tieši proporcionāls loga laukumam S un temperatūras starpībai ΔT starp iekšējo un ārējo stiklu un apgriezti proporcionāls tā biezumam d:

dQ/dt = A S/d ∆T

8. Difūzijas fenomens ir līdzsvara sadalījuma noteikšanas process

Koncentrēšanās fāzēs. Difūzija iet uz sāniem, izlīdzinot koncentrācijas.

m = D ∆c/∆x c – koncentrācija
m = D c׳x x - koordinēt, D- difūzijas koeficients

Fika likums:

9. Bija zināms, ka elektriskais lauks uzbudina vai nu elektriskie lādiņi, vai magnētiskais lauks, kuram ir viens avots – elektriskā strāva. Džeimss Klārks Maksvels ieviesa vienu grozījumu elektromagnētisma likumos, kas tika atklāti pirms viņa: magnētiskais lauks rodas arī tad, kad elektriskais lauks. No pirmā acu uzmetiena nelielam grozījumam bija grandiozas sekas: parādījās pilnīgi jauns fizisks objekts, kaut arī pildspalvas galā, elektromagnētiskais vilnis. Maksvelam meistarīgi piederēja, atšķirībā no Faradeja, kurš šķita iespējama tā pastāvēšana, secināja elektriskā lauka vienādojumu:

∂E/∂x = M∂B/Mo ∂t Mo = konst. t

Elektriskā lauka izmaiņas izraisa magnētiskā lauka parādīšanos jebkurā telpas punktā, citiem vārdiem sakot, elektriskā lauka izmaiņu ātrums nosaka magnētiskā lauka lielumu. Zem lielas elektriskās strāvas - liels magnētiskais lauks.

IV. Pētīto konsolidācija

– Mēs pētījām atvasinājumu un tā īpašības. Gribētos izlasīt Gilberta filozofisko izteikumu: “Katram cilvēkam ir noteikts skatījums. Kad šis horizonts sašaurinās līdz bezgalīgi mazam, tas pārvēršas par punktu. Tad cilvēks saka, ka tas ir viņa viedoklis.
Mēģināsim izmērīt skatījumu uz atvasinājuma pielietojumu!

Zemes gabals "Lapa"(atvasinājuma pielietojums bioloģijā, fizikā, dzīvē)

Uzskatiet kritienu par nevienmērīgu kustību atkarībā no laika.

Tātad: S = S(t) V = S′(t) = x′(t), a = V′(t) = S″(t)

(Teorētiskā aptauja: atvasinājuma mehāniskā nozīme).

1. Problēmu risināšana

Atrisiniet problēmas patstāvīgi.

2. F = ma F = mV′ F = mS″

Uzrakstīsim Portona II likumu un, ņemot vērā atvasinājuma mehānisko nozīmi, pārrakstīsim to formā: F = mV′ F = mS″

Filmas "Vilki, goferi" sižets

Atgriezīsimies pie vienādojumiem: Apsveriet eksponenciālās izaugsmes un samazinājuma diferenciālvienādojumus: F = ma F = mV" F = mS""
Daudzu problēmu risinājums fizikā, tehniskajā bioloģijā un sociālajās zinātnēs tiek reducēts uz funkciju atrašanas problēmu f"(x) = kf(x), apmierinot diferenciālvienādojumu, kur k = konst .

Cilvēka formula

Cilvēks ir tikpat reižu lielāks par atomu, cik mazāks par zvaigzni:

No tā izriet, ka
Šī ir formula, kas nosaka cilvēka vietu Visumā. Saskaņā ar to cilvēka izmēri atspoguļo zvaigznes un atoma vidējo proporcionālo vērtību.

Nodarbību es vēlētos noslēgt ar Lobačevska vārdiem: "Nav nevienas matemātikas jomas, lai cik abstrakta tā būtu, kas kādreiz nebūtu attiecināma uz reālās pasaules parādībām."

V. Kolekcijas skaitļu risinājums:

Patstāvīga problēmu risināšana uz padomes, kolektīva problēmu risinājumu analīze:

№ 1 Atrodi materiālā punkta ātrumu 3. sekundes beigās, ja punkta kustību uzrāda vienādojums s = t^2 –11t + 30.

№ 2 Punkts kustas taisni saskaņā ar likumu s = 6t – t^2. Kurā brīdī tā ātrums būs nulle?

№ 3 Divi ķermeņi kustas taisnā līnijā: viens pēc likuma s \u003d t^3 - t^2 - 27t, otrs - pēc likuma s \u003d t^2 + 1. Nosakiet brīdi, kad šo ķermeņu ātrumi. ķermeņi ir vienādi.

№ 4 Automašīnai, kas pārvietojas ar ātrumu 30 m/s, bremzēšanas ceļu nosaka pēc formulas s(t) =30t-16t^2, kur s(t) ir attālums metros, t ir bremzēšanas laiks sekundēs. . Cik ilgs laiks nepieciešams, lai samazinātu ātrumu, līdz automašīna pilnībā apstājas? Kāds ir automašīnas nobrauktais attālums no bremzēšanas sākuma līdz pilnīgai apstāšanās brīdim?

№5 Ķermenis ar masu 8 kg kustas pa taisnu pēc likuma s = 2t^2+ 3t - 1. Atrast ķermeņa kinētisko enerģiju (mv^2/2) 3 sekundes pēc kustības sākuma.

Risinājums: Atrodiet ķermeņa ātrumu jebkurā laikā:
V=ds/dt=4t+3
Aprēķiniet ķermeņa ātrumu laikā t = 3:
V t \u003d 3 \u003d 4 * 3 + 3 \u003d 15 (m/s).
Noteiksim ķermeņa kinētisko enerģiju laikā t = 3:
mv2/2 = 8 - 15^2 /2 = 900 (J).

№6 Atrast ķermeņa kinētisko enerģiju 4 s pēc kustības sākuma, ja tā masa ir 25 kg, un kustības likums ir s = 3t^2-1.

№7 Ķermenis, kura masa ir 30 kg, kustas taisnā līnijā saskaņā ar likumu s = 4t^2 + t. Pierādīt, ka ķermeņa kustība notiek pastāvīga spēka iedarbībā.
Risinājums: Mums ir s" = 8t + 1, s" = 8. Tāpēc a(t) = 8 (m/s^2), t.i., ar doto kustības likumu ķermenis kustas ar nemainīgu 8 m paātrinājumu /s^2. Turklāt, tā kā ķermeņa masa ir nemainīga (30 kg), tad saskaņā ar Ņūtona otro likumu spēks, kas uz to iedarbojas F = ma = 30 * 8 = 240 (H), arī ir nemainīga vērtība.

№8 Ķermenis ar masu 3 kg kustas pa taisni saskaņā ar likumu s(t) = t^3 - 3t^2 + 2. Atrast spēku, kas iedarbojas uz ķermeni laikā t = 4s.

№9 Materiālais punkts pārvietojas saskaņā ar likumu s = 2t^3 – 6t^2 + 4t. Atrodiet tā paātrinājumu 3. sekundes beigās.

VI. Atvasinājuma pielietojums matemātikā:

Atvasinājums matemātikā parāda lieluma izmaiņu pakāpes skaitlisko izteiksmi, kas atrodas vienā punktā dažādu apstākļu ietekmē.

Atvasinātā formula datēta ar 15. gadsimtu. Lielais itāļu matemātiķis Tartaglija, apsverot un attīstot jautājumu - cik lielā mērā šāviņa darbības rādiuss ir atkarīgs no ieroča slīpuma, to izmanto savos rakstos.

Atvasinātā formula bieži sastopama slavenu 17. gadsimta matemātiķu darbos. To izmanto Ņūtons un Leibnics.

Pazīstamais zinātnieks Galileo Galilejs velta veselu traktātu par atvasinājuma lomu matemātikā. Tad atvasinājums un dažādas prezentācijas ar tā pielietojumu sāka atrasties Dekarta, franču matemātiķa Robervala un angļa Gregorija darbos. Lielu ieguldījumu atvasinājuma izpētē sniedza tādi prāti kā Lopitāls, Bernulli, Langrange un citi.

1. Uzzīmējiet un izpētiet funkciju:

Šīs problēmas risinājums:

Relaksācijas brīdis

VII. Atvasinājuma pielietojums fizikā:

Pētot noteiktus procesus un parādības, bieži rodas problēma noteikt šo procesu ātrumu. Tā risinājums noved pie atvasinājuma jēdziena, kas ir diferenciālrēķina pamatjēdziens.

Diferenciālrēķina metode tika izveidota 17. un 18. gadsimtā. Divu izcilu matemātiķu vārdi I. Ņūtons un G.V. Leibnica.

Ņūtons nonāca pie diferenciālrēķina atklāšanas, risinot uzdevumus par materiāla punkta ātrumu noteiktā laika momentā (momentānais ātrums).

Fizikā atvasinājumu galvenokārt izmanto, lai aprēķinātu lielāko vai mazākās vērtības jebkādus daudzumus.

Problēmu risināšana:

№1 Potenciālā enerģija U daļiņas laukam, kurā ir cita, tieši tāda pati daļiņa, ir šāda forma: U = a/r 2 – b/r, kur a un b ir pozitīvas konstantes, r- attālums starp daļiņām. Atrodi: a) vērtību r0 kas atbilst daļiņas līdzsvara stāvoklim; b) noskaidrot, vai šī situācija ir stabila; iekšā) Fmaks pievilkšanas spēka vērtība; d) attēlo aptuvenus atkarības grafikus U(r) un F(r).

Šīs problēmas risinājums: noteikt r0 kas atbilst daļiņas līdzsvara stāvoklim, mēs pētām f = U(r) līdz galējībai.

Izmantojot attiecības starp lauka potenciālo enerģiju

U un F, tad F = -dU/dr, saņemam F = – dU/dr = – (2a/r3+ b/r2) = 0; kurā r = r0; 2a/r3 = b/r2 => r0 = 2a/b; Stabilu vai nestabilu līdzsvaru nosaka otrā atvasinājuma zīme:
d2U/dr02= dF/dr0 = – 6a/r02 + 2b/r03 = – 6a/(2a/b)4 + 2b/(2a/b)3 = (– b4/8a3)< 0 ;
līdzsvars ir stabils.

Lai noteiktu Fmaks pievilcību, es izpētu funkciju ekstrēmiem: F = 2a/r3 - b/r2;
dF/dr = –6a/r4 + 2b/r3 = 0; plkst r = r1 = 3a/b; aizstājot, es saprotu Fmax = 2a/r31 – b/r31 = – b3/27a2; U(r) = 0; plkst r = a/b; U(r)min plkst r = 2, a/b = r0;F = 0; F(r)maks plkst r = r1 = 3a/b;
Atbilde: F(r)maks plkst r = r1 = 3a/b;

№2 Ķēde ar ārējo pretestību R = 0,9 omi darbina ar akumulatoru k = 36 identiski avoti, no kuriem katram ir emf E=2 AT un iekšējā pretestība r0 = 0,4 omi. Akumulators iekļauts n paralēli savienotas grupas, un katra no tām satur m sērijveidā savienotas baterijas. Par kādām vērtībām m, n saņems maksimumu Džārējā R.

Šīs problēmas risinājums:

Kad baterijas ir savienotas virknē E gr = m* E ; rgr = r0*m;
un ar paralēlu savienojumu rbat = r0m/n; E bats = m* E,
Oma likums J=m E /(R+ r0m/n) = m E n/(nR + r0m)
Jo k ir kopējais bateriju skaits, tad k = mn;
J=k E /(nR + r0m) = k E /(nR + kr0/n);
Lai atrastu nosacījumu, saskaņā ar kuru Dž strāva ķēdē maksimāli izpētīt funkciju J = J(n) ekstrēmu, ņemot atvasinājumu attiecībā pret n un pielīdzinot to nullei.
J'n - (k E (R - kr0/n2))/ (nR + kr0/n)2 = 0;
n2 = kr/R
n = √kr/R = √3,6*0,4/0,9 = 4;
m = k/n = 36/4 = 9;
kurā Jmax = k E / (nR + mr0) \u003d 36 * 2 / (4 * 0,9 + 9 * 0,4) \u003d 10 A;

Atbilde: n = 4, m = 9.

№3 Masu platforma M pastāvīga spēka iedarbībā sāk virzīties pa labi F. Smiltis uz tās lej no stacionāra bunkura. Iekraušanas ātrums ir nemainīgs un vienāds ar µ kg/s. Neņemot vērā berzi, atrodiet atkarību no platformas paātrinājuma laika a iekraušanas laikā. Nosakiet paātrinājumu a1 platforma gadījumā, ja smiltis netiek uzbērtas uz platformas, bet no piepildītās platformas tās ar nemainīgu ātrumu izplūst caur caurumu tās dibenā µ kg/s.

Šīs problēmas risinājums: vispirms apsveriet gadījumu, kad uz platformas tiek uzbērtas smiltis
Platformas-smilšu sistēmas kustību var aprakstīt, izmantojot Ņūtona otro likumu:
dP/dt = FΣ
P ir platformas-smilšu sistēmas impulss, FΣ ir spēks, kas iedarbojas uz platformas-smilšu sistēmu.
Ja cauri lpp apzīmē platformas impulsu, tad varam rakstīt: dp/dt = F
Ļaujiet mums atrast platformas impulsa izmaiņas bezgalīgi mazā laika intervālā Δ t: Δ p = (M + µ(t + Δ t))(u +Δ u) – (M + µt)u = FΔ t;
kur u- platformas ātrums.
Atverot iekavas un veicot samazinājumus, mēs iegūstam:
Dp = µuΔ t+MΔ u+ Δ µut +Δ µuΔ t = FΔ t
Sadaliet ar Δt un pārejiet uz robežu Δ t→ 0
Mdu/dt + µtdu/dt + µu= F vai d[(M + µt)u]/dt = F
Šo vienādojumu var integrēt, pieņemot, ka platformas sākotnējais ātrums ir nulle: (M + µt)u = Ft.
Sekojoši: u = Ft/(M + µt)
Pēc tam platformas paātrinājums: a = du/dt = (F(M + µt) – Ftµ)/(M + µt) 2 = FM / (M + µt) 2

Apsveriet gadījumu, kad smiltis izplūst no piepildītas platformas.
Impulsa izmaiņas īsā laika periodā:
Δ p = (M – µ(t +Δ t))(u+Δ u) +Δ µtu – (M – µt)u = FΔ t
Termins Δ µtu ir smilšu daudzuma impulss, kas izlijis no platformas laikā Δ t. Pēc tam:
Δ p = MΔ u-µtΔ u-Δ µtΔ u=FΔ t
Sadaliet ar Δ t un pāriet līdz robežai Δ t→ 0
(M – µt)du/dt = F
Or a1 = du/dt = F/(M – µt)

Atbilde: a = FM / (M + µt) 2, a1 = F/(M - µt)

VIII.Patstāvīgais darbs:

Atrodiet funkciju atvasinājumus:

Līnija y \u003d 2x ir pieskares funkcijai: y \u003d x 3 + 5x 2 + 9x + 3. Atrodiet saskares punkta abscisu.

IX. Apkopojot nodarbību:

– Kādas bija nodarbības tēmas?
- Ko tu iemācījies stundā?
Kādi teorētiskie fakti tika apkopoti nodarbībā?
– Kādi bija visgrūtākie uzdevumi? Kāpēc?

Bibliogrāfija:

1. Ameļkins V.V., Sadovskis A.P. Matemātiskie modeļi un diferenciālvienādojumi. - Minska: Augstskola, 1982. - 272 lpp.
2. Amelkins V.V. Diferenciālvienādojumi lietojumos. M.: Zinātne. Fizikālās un matemātiskās literatūras galvenais izdevums, 1987. - 160 lpp.
3. Erugins N.P. Grāmata lasīšanai par diferenciālvienādojumu vispārējo kursu. - Minska: Zinātne un tehnoloģija, 1979. - 744 lpp.
4. .Žurnāls "Potenciāls" 2007. gada novembris №11
5. "Algebra un analīzes sākums" 11. klase S.M. Nikoļskis, M.K. Potapovs un citi.
6. "Algebra un matemātiskā analīze" N.Ya. Viļenkins un citi.
7. "Matemātika" V.T. Lisičkins, I.L. Soloveichik, 1991. gads

Uzdevums. Izmaksu funkcijai ir forma un ražošanas ienākumi X preču vienības ir definētas šādi:

Nosakiet ražotāja optimālo izvades vērtību x0.

Risinājums:

Peļņa P(x) =D(x) - C(x), kur D(x) - ienākumi no ražošanas X produktu vienības.

Peļņas funkcija izskatās šādi:

Atrodiet peļņas funkcijas atvasinājumu:

Acīmredzot P "(x)> 0 plkst X< 100 tātad augstākā vērtība segmentā ir peļņa R(100) = 399 900. Tagad atradīsim lielāko peļņas vērtību intervālā (100; + ∞). Ir viens kritisks punkts x= 200. Tajā pašā laikā P "(x)> 0 pie 100< x < 200 и R" (X)< 0 plkst x> 200, t.i. x= 200 - maksimālā vērtība P(x) uz intervāla (100; + ∞).

R(200) = 419 900 > R(100), tātad x vairumtirdzniecība = 200 (vienība).

Uzdevums. Cementa rūpnīca saražo X tonnas cementa dienā. Saskaņā ar līgumu viņam katru dienu jāpiegādā būvfirmai vismaz 20 tonnas cementa. Rūpnīcas ražošanas jauda ir tāda, ka cementa produkcija nevar pārsniegt 90 tonnas dienā.

Nosakiet, pie kāda ražošanas apjoma vienības izmaksas būs vislielākās (mazākās), ja izmaksu funkcijai ir šāda forma:

K=-x3+98x2+200x. Vienības izmaksas būs K/x=-x2+98x+200

Risinājums:

Problēma tiek samazināta līdz funkcijas lielāko un mazāko vērtību atrašanai

y= - x2+98x+200. Starp.

DIV_ADBLOCK1021">

6 Atvasinājuma pielietojums medicīnā

Diferenciālrēķina pielietojums medicīnā tiek samazināts līdz ātruma aprēķināšanai. Piemēram, atveseļošanās reakciju ātrums un relaksācijas procesa ātrums.

Organisma reakcija uz ievadītajām zālēm var izpausties kā asinsspiediena paaugstināšanās, ķermeņa temperatūras izmaiņas, pulsa vai citu fizioloģisku rādītāju izmaiņas. Reakcijas pakāpe ir atkarīga no izrakstītajām zālēm, to devas. Izmantojot atvasinājumu, jūs varat aprēķināt, pie kādas zāļu devas ķermeņa reakcija ir maksimālā. Ar otrā atvasinājuma palīdzību ir iespējams noteikt apstākļus, kādos procesa ātrums ir visjutīgākais pret jebkādām ietekmēm

Uzdevums Izliksimies tā X apzīmē izrakstīto zāļu devu, plkst ir reakcijas pakāpes funkcija. y=f(x)=x²(a-x), kur a ir kāda pozitīva konstante. Par kādu vērtību X maksimālā atsaucība?

Risinājums:

https://pandia.ru/text/80/244/images/image137_6.gif" width="116" height="24">. Pēc tam ar ..gif" width="49" height="42"> - devas līmenis, kas nodrošina maksimālo reakciju.

Līkuma punkti ir svarīgi bioķīmijā, jo tie nosaka apstākļus, kādos kāds daudzums, piemēram, procesa ātrums, ir visjutīgākais (vai vismazāk) pret jebkādām ietekmēm.

Uzdevums. Ievērojama asins zuduma rezultātā dzelzs saturs asinīs samazinājās par 210 mg. Dzelzs deficīts sakarā ar tā atjaunošanos laika gaitā t samazinās atbilstoši likumam mg (t - diena). Atrodiet atkarību no dzelzs atgūšanas ātruma asinīs laikā. Aprēķiniet šo ātrumu šobrīd t=0 un pēc 7 dienām.

Risinājums:

Dzelzs atgūšanas ātrums:

https://pandia.ru/text/80/244/images/image144_5.gif" width="33" height="18"> atveseļošanās ātrums ir 30 mg dienā. Pēc 7 dienām atveseļošanās ātrums ir 11,1 mg /diena dienas:

Relaksācijas process ir process, kurā sistēma tiek atgriezta stabilā līdzsvara stāvoklī, no kura tā tika pārņemta. Daudzos gadījumos (īpaši ar vienu ekspozīciju) šo procesu apraksta ar eksponenciālo vienādojumu. Tā fiziskā nozīme ir: - tas ir laiks, kurā Pētniecības aktivitātes sākotnējā novirze" href="/text/category/nauchno_issledovatelmzskaya_deyatelmznostmz/" rel ="bookmark">pētniecības un ražošanas darbība. Piemēram, procesu inženieri ķīmiskās ražošanas efektivitātes noteikšanā, ķīmiķi, kas izstrādā zāles medicīnai un lauksaimniecībai, kā arī ārsti un agronomi, kuri lieto šīs zāles cilvēku ārstēšanai un iestrādei augsnē. Dažas reakcijas ir gandrīz tūlītējas, bet citas ir ļoti lēnas. AT īsta dzīve lai atrisinātu ražošanas problēmas medicīnas, lauksaimniecības un ķīmiskajā rūpniecībā, ir svarīgi zināt ķīmisko vielu reakcijas ātrumus.

Ļaujiet funkcijai m=m(t), kur m- vielas daudzums, kas vienā reizē ir iestājies ķīmiskā reakcijā t. Laika pieaugums Δt sakritīs ar pieaugumu ∆m daudzumus m. Attieksme ∆m/∆t ir ķīmiskās reakcijas vidējais ātrums noteiktā laika periodā Δt. Šīs attiecības robeža, cenšoties Δt līdz nullei ir ķīmiskās reakcijas ātrums noteiktā laikā.

Uzdevums. Sakarība starp kādas ķīmiskas reakcijas rezultātā iegūtas vielas masu x un laiku t izteikts ar vienādojumu https://pandia.ru/text/80/244/images/image151_5.gif" width="283" height="30 src=">

Uzdevums.Šķīduma koncentrācija laika gaitā mainās saskaņā ar likumu: . Atrodiet izšķīšanas ātrumu.

Risinājums:

Izšķīdināšanas ātrumu aprēķina, izmantojot atvasinājumu:

https://pandia.ru/text/80/244/images/image154_4.gif" width="139" height="42 src=">. Iegūstiet formulu iedzīvotāju skaita pieauguma tempam.

Risinājums:

Uzdevums. Dienas izslaukuma atkarība y litros no govju vecuma X gados nosaka ar vienādojumu , kur x>2. Atrodiet slaucamo govju vecumu, kurā dienas izslaukums būs vislielākais.

Risinājums:

https://pandia.ru/text/80/244/images/image161_4.gif" width="77" height="23 src=">

(gadi) - maksimālais punkts, slaucamo govju vecums, pie kura dienas izslaukums būs lielākais.

Secinājums

Šajā rakstā apskatīts viens no svarīgākajiem matemātiskās analīzes jēdzieniem - funkcijas atvasinājums no tās viedokļa. praktisks pielietojums. Ar atvasinājuma palīdzību jūs varat atrisināt ļoti dažādas problēmas, kas saistītas ar jebkuru jomu. cilvēka darbība. Jo īpaši ar atvasinājumu palīdzību iespējams detalizēti izpētīt funkcijas, precīzāk konstruēt to grafikus, atrisināt vienādojumus un nevienādības, pierādīt identitātes un nevienādības, kā arī atrast lielumu lielākās un mazākās vērtības.

Visām iepriekš minētajām atvasinājuma pielietošanas jomām ir atlasīti un apkopoti aptuveni divi simti problēmu. Katra krājuma sadaļa sākas ar īsu teorētisko pamatu kopsavilkumu, satur tipiski uzdevumi ar risinājumiem un vingrinājumu komplektiem priekš neatkarīgs lēmums. Šie uzdevumi paplašina redzesloku un palielina interesi par atvasinājumu. Tie var būt interesanti un noderīgi skolēniem, kuriem patīk matemātika.

Literatūra

1. Bogomolova uzdevumi matemātikā: mācību grāmata koledžām. – M.: Bustards, 2005.

2. Bogomolovs: mācību grāmata. koledžām /, - M .: Bustard, 2010.

3. Bogomolovs. Didaktiskie uzdevumi: mācību grāmata. pabalsts koledžām /, - M .: Bustard, 2005.

4. Istomina: jautājumi un atbildes: mācību grāmata. pabalsts augstskolām. - Rostova n / a: Fēnikss, 2002.

5. Lisičkins: mācību grāmata. pabalsts tehnikumiem /, - M.: Augstākā. skola, 1991.

6. Nikoļska matemātiskā analīze: mācību grāmata. pabalsts studentiem. ssuzov.- M.: Bustard, 2012. gads.

7. Omeļčenko: mācību grāmata. pabalsts koledžām. - Rostova n / a: Fēnikss, 2007.

8. Fiļimonova: mācību grāmata. pabalsts koledžām. – Rostova n/a: Fēnikss, 2013.