Popis prezentácie na jednotlivých snímkach:

1 snímka

Popis snímky:

Téma hodiny: Aplikácia derivácie v rôznych oblastiach vedomostí Učiteľ matematiky MBOU "Škola č. 74" Zagumennova Marina Vladimirovna

2 snímka

Popis snímky:

Účel lekcie: Naučiť sa hlavné oblasti použitia derivátu v rôznych oblastiach vedy a techniky; Zvážte na príkladoch riešenia praktických problémov, ako sa derivát používa v chémii, fyzike, biológii, geografii a ekonómii.

3 snímka

Popis snímky:

"Neexistuje jediná oblasť matematiky, akokoľvek abstraktná môže byť, ktorá sa jedného dňa nebude dať použiť na javy skutočného sveta." N.I. Lobačevského

4 snímka

Popis snímky:

Pravidlá diferenciácie Derivácia súčtu O konštantnom činiteľovi Derivácia súčinu Derivácia zlomku Derivácia komplexnej funkcie (u+v)"= u" + v' (Cu)"=Cu' (uv)"=u"v +uv' (u/v)" =(u"v-uv")/v2 hꞌ(x)=gꞌ(f(x))f ꞌ(x)

5 snímka

Popis snímky:

Úloha derivácie vo fyzike. Pohyb auta pri brzdení je opísaný vzorcom s(t) = 30t - 5t2, (s je brzdná dráha v metroch, t je čas v sekundách od začiatku brzdenia po úplné zastavenie auta). Zistite, koľko sekúnd je auto v pohybe od okamihu, keď začne brzdiť, až po úplné zastavenie. Akú vzdialenosť prejde auto od začiatku brzdenia až po úplné zastavenie? Riešenie: Keďže rýchlosť je prvou deriváciou pohybu v čase, potom v = S'(t) = 30 - 10t, pretože pri brzdení je rýchlosť nulová, potom 0=30–10t; 10t = 30; t = 3 (s). Brzdná dráha S(t) = 30t - 5t2 = 30∙3-5∙32 = 90-45 = 45(m). Odpoveď: čas spomalenia 3s, brzdná dráha 45m.

6 snímka

Popis snímky:

To je zaujímavé Parník „Chelyuskin“ vo februári 1934 úspešne prešiel celou severnou námornou cestou, ale v r. Beringov prieliv bol uväznený v ľade. Ľad odniesol Čeľuskina na sever a rozdrvil ho. Tu je popis katastrofy: „Silný kov trupu nepodľahol okamžite,“ hlásil v rádiu šéf expedície O.Yu. Schmidt. - Bolo vidieť, ako bola ľadová kryha vtlačená do boku a ako sa plášte nad ňou vyduli a ohýbali von. Ľad pokračoval v pomalom, no nezadržateľnom napredovaní. Napuchnuté železné plechy oplechovania trupu boli roztrhané vo švíkoch. Nity odleteli s prasknutím. V okamihu sa odtrhla ľavá strana lode od predného priestoru až po zadný koniec paluby... „Prečo sa stala katastrofa?

7 snímka

Popis snímky:

Sila tlaku ľadu Р sa rozloží na dve časti: F a R. R je kolmá na dosku, F smeruje tangenciálne. Uhol medzi P a R - α - uhol strany k vertikále. Q je sila trenia ľadu o dosku. Q = 0,2 R (0,2 je koeficient trenia). Ak Q< F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q >F, potom trenie zabraňuje kĺzaniu ľadovej kryhy a ľad môže rozdrviť a tlačiť dosku. 0,2 R< R tgα , tgα >0,2; Q< F, если α >1100. Sklon bokov lode voči vertikále pod uhlom α > 1100 zaisťuje bezpečnú plavbu v ľade.

8 snímka

Popis snímky:

Derivát v chémii Derivát v chémii sa používa na určenie rýchlosti chemická reakcia. Je to potrebné pre: procesných inžinierov pri určovaní účinnosti chemickej výroby, chemikov vyvíjajúcich lieky pre medicínu a poľnohospodárstvo, ako aj lekári a agronómovia, ktorí tieto lieky používajú na liečbu ľudí a aplikujú ich do pôdy. Na vyriešenie výrobných problémov v medicínskom, poľnohospodárskom a chemickom priemysle je jednoducho potrebné poznať reakčné rýchlosti chemikálií.

9 snímka

Popis snímky:

Úloha z chémie Nech je množstvo látky, ktoré vstúpilo do chemickej reakcie, dané závislosťou: р(t) = t2/2 + 3t –3 (mol). Nájdite rýchlosť chemickej reakcie po 3 sekundách. Odkaz: Rýchlosť chemickej reakcie je zmena koncentrácie reaktantov za jednotku času alebo derivácia koncentrácie reaktantov vzhľadom na čas (v jazyku matematiky by koncentrácia bola funkcia a čas by bol argument )

10 snímka

Popis snímky:

Riešenie Pojem v jazyku chémie Zápis Pojem v jazyku matematiky Látkové množstvo v čase t0 p = p(t0) Funkcia Časový interval ∆t = t – t0 Prírastok argumentu Zmena látkového množstva ∆p = p(t0+ ∆ t) – p(t0) Prírastok funkcie Priemerná rýchlosť chemickej reakcie ∆p/∆t Pomer prírastku funkcie k prírastku argumentu V (t) = p'(t)

11 snímka

Popis snímky:

Derivát v biológii Úloha v biológii: Na základe známej závislosti veľkosti populácie x(t) určte relatívny rast v čase t. Referencia: Populácia je súbor jedincov daného druhu, ktorý zaberá určitú oblasť územia v rámci rozsahu druhu, voľne sa navzájom kríži a je čiastočne alebo úplne izolovaný od iných populácií a je tiež základnou jednotkou. evolúcie.

12 snímka

Popis snímky:

Riešenie Koncept v jazyku biológie Notácia Koncept v jazyku matematiky Populácia v čase tx = x(t) Funkcia Časový interval ∆t = t – t0 Prírastok argumentu Zmena populácie ∆x = x(t) – x(t0) Prírastok funkcie Rýchlosť zmeny veľkosti populácie ∆x/∆t Pomer prírastku funkcie k prírastku argumentu Relatívny rast v danom momente lim∆x/∆t ∆t → 0 Derivácia Р = x" (t)

13 snímka

Popis snímky:

14 snímka

Popis snímky:

Derivácia v geografii Derivácia pomáha vypočítať: Niektoré hodnoty v seizmografii Vlastnosti elektromagnetického poľa Zemská rádioaktivita jadrových geofyzikálnych ukazovateľov Mnoho hodnôt v ekonomickej geografii Odvoďte vzorec na výpočet populácie na území v čase t.

15 snímka

Popis snímky:

Geografický problém Odvoďte vzorec na výpočet populácie na obmedzenom území v čase t.

16 snímka

Popis snímky:

Riešenie Nech y=y(t) je populácia. Uvažujme populačný rast pre ∆t = t – t0 ∆у = k∙y∙∆t, kde k = kр – kс je miera rastu populácie, (kр je pôrodnosť, kс je úmrtnosť). ∆у/∆t = k∙y ako ∆t → 0 dostaneme lim ∆у/∆t = у’. Rast populácie - y’ = k∙y. ∆t → 0 Záver: derivácia v geografii je kombinovaná s mnohými jej odvetviami (seizmografia, poloha a počet obyvateľov), ako aj s ekonomickou geografiou. To všetko umožňuje plnšie študovať vývoj obyvateľstva a krajín sveta.

17 snímka

Popis snímky:

Derivát v ekonómii Derivát rieši dôležité otázky: Akým smerom sa zmenia príjmy vlády zvýšením daní alebo zavedením ciel? Zvýši sa alebo zníži príjem firmy, keď sa zvýši cena jej produktov? Na vyriešenie týchto otázok je potrebné zostrojiť spojovacie funkcie vstupných premenných, ktoré sú následne študované metódami diferenciálneho počtu. Pomocou extrému funkcie v ekonomike možno tiež nájsť najvyššiu produktivitu práce, maximálny zisk, maximálny výkon a minimálne náklady.

18 snímka

Popis snímky:

Problém v ekonómii č. 1 (výrobné náklady) Nech y sú výrobné náklady a x je množstvo produkcie, potom x1 je zvýšenie výroby a y1 je zvýšenie výrobných nákladov.

19 snímka

Popis snímky:

20 snímka

Prezentácia na tému: "Využitie derivátu vo vede av živote"Účinkuje študentka skupiny Phi-17 Dolzhenkova Anastasia Informácie z histórie vzhľadu derivátu: Slogan mnohých matematikov XVII storočia. bolo: "Posuň sa vpred a viera v správnosť výsledkov sa k tebe dostaví." Termín "derivát" - ​​(francúzsky odvodiť - za, za) zaviedol v roku 1797 J. Lagrange. Zaviedol aj modernú notáciu r" , f'. označenie lim je skratkou latinského slova limes (hranica, hranica). Termín „limit“ zaviedol I. Newton. I. Newton nazval deriváciu tokom a samotnú funkciu - plynulosť. G. Leibniz hovoril o diferenciálnom vzťahu a deriváciu označil takto: Lagrange Joseph Louis (1736-1813) francúzsky matematik a mechanik Newton:

„Tento svet bol zahalený hlbokou tmou. Nech je svetlo! A tu prichádza Newton. A. Pogue.

Isaac Newton (1643-1727) jeden z tvorcov diferenciálneho počtu.

Jeho hlavné dielo, Matematické princípy prírodnej filozofie, malo obrovský vplyv na rozvoj prírodných vied a stalo sa prelomovým bodom v dejinách prírodných vied.

Newton predstavil pojem derivát, študoval zákony mechaniky, čím odhalil jeho mechanický význam.

Čo je to derivácia funkcie?

Derivácia funkcie v danom bode je limitom pomeru prírastku funkcie v tomto bode k prírastku argumentu, keď má prírastok argumentu tendenciu k nule.

Fyzikálny význam derivátu.

• Rýchlosť je derivácia vzdialenosti vzhľadom na čas:
v(t) = S'(t)

• Zrýchlenie je derivácia rýchlosti vzhľadom na čas:

a(t) = v′(t) = S′′(t)

Geometrický význam derivácie: Smernica dotyčnice ku grafu funkcie sa rovná derivácii tejto funkcie, vypočítanej v bode dotyku. f′(x) = k = tga Derivát v elektrotechnike:

V našich domovoch, v doprave, v továrňach: elektrický prúd funguje všade. Pod elektrickým prúdom rozumieme usmernený pohyb voľných elektricky nabitých častíc.

Kvantitatívna charakteristika elektrického prúdu je sila prúdu.

V obvode elektrického prúdu sa elektrický náboj v priebehu času mení podľa zákona q=q (t). Prúd I je deriváciou náboja q vzhľadom na čas.

V elektrotechnike sa využíva najmä práca striedavý prúd.

Elektrický prúd, ktorý sa mení s časom, sa nazýva striedavý prúd. Obvod striedavého prúdu môže obsahovať rôzne prvky: ohrievače, cievky, kondenzátory.

Získanie striedavého elektrického prúdu je na základe zákona elektromagnetická indukcia, ktorého formulácia obsahuje derivát magnetického toku.

Derivát v chémii:

• A v chémii našiel diferenciálny počet široké uplatnenie na zostavovanie matematických modelov chemických reakcií a následný popis ich vlastností.
• Chémia je veda o látkach, chemických premenách látok.
• Chémia študuje vzorce rôznych reakcií.
• Rýchlosť chemickej reakcie je zmena koncentrácie reaktantov za jednotku času.
• Pretože sa rýchlosť reakcie v počas procesu neustále mení, zvyčajne sa vyjadruje ako derivát koncentrácie reaktantov v čase.

Derivát v geografii:

Myšlienka sociologického modelu Thomasa Malthusa je taká, že rast populácie je úmerný počtu obyvateľov v danom čase t až N(t), . Malthusiánsky model dobre fungoval na opis populácie Spojených štátov v rokoch 1790 až 1860. Tento model už vo väčšine krajín neplatí.

Integrál a jeho aplikácia: Trochu histórie: História pojmu integrál siaha až k matematikom Staroveké Grécko a Staroveký Rím. Práca vedca starovekého Grécka - Eudoxus z Knidos (asi 408-asi 355 pred Kristom) je známa tým, že zisťuje objemy tiel a vypočítava plochy plochých postáv. Integrálny počet sa rozšíril v 17. storočí. Vedci: G. Leibniz (1646-1716) a I. Newton (1643-1727) objavili nezávisle na sebe a takmer súčasne vzorec, neskôr nazývaný Newton-Leibniz vzorec, ktorý používame. To, že filozof a fyzik vymysleli matematický vzorec, nikoho neprekvapuje, pretože matematika je jazyk, ktorým hovorí samotná príroda. Integrálny počet sa rozšíril v 17. storočí. Vedci: G. Leibniz (1646-1716) a I. Newton (1643-1727) objavili nezávisle na sebe a takmer súčasne vzorec, neskôr nazývaný Newton-Leibniz vzorec, ktorý používame. To, že filozof a fyzik vymysleli matematický vzorec, nikoho neprekvapuje, pretože matematika je jazyk, ktorým hovorí samotná príroda. Zadaný symbol Zadaný symbol Leibniz (1675). Tento znak je variáciou latinského písmena S (prvé písmeno slova súčet). Samotné slovo integrálne vynájdený J. Bernoulli (1690). Pravdepodobne pochádza z latinského integero, čo v preklade znamená obnoviť predchádzajúci stav, obnoviť. Hranice integrácie naznačil už L. Euler (1707-1783). V roku 1697 sa objavil názov nového odvetvia matematiky - integrálny počet. Zaviedol ho Bernoulli. V matematickej analýze je integrál funkcie rozšírením pojmu súčtu. Proces hľadania integrálu sa nazýva integrácia. Tento proces sa zvyčajne používa pri hľadaní veličín ako plocha, objem, hmotnosť, posunutie atď., kedy je daná rýchlosť alebo rozloženie zmien tejto veličiny vzhľadom na nejakú inú veličinu (poloha, čas a pod.).Čo je integrál? Integrál je jedným z najdôležitejších pojmov matematická analýza , ktorý vzniká pri riešení problémov hľadania plochy pod krivkou, prejdenej vzdialenosti pri nerovnomernom pohybe, hmotnosti nehomogénneho telesa a pod., ako aj pri probléme obnovy funkcie podľa nej derivát Vedci sa snažia vyjadriť všetky fyzikálne javy vo forme matematického vzorca. Keď máme vzorec, môžeme ho použiť na výpočet čohokoľvek. A integrál je jedným z hlavných nástrojov na prácu s funkciami. Vedci sa snažia vyjadriť všetky fyzikálne javy vo forme matematického vzorca. Keď máme vzorec, môžeme ho použiť na výpočet čohokoľvek. A integrál je jedným z hlavných nástrojov na prácu s funkciami. Integračné metódy:

• Tabuľkový.
• Redukcia na tabuľkovú transformáciu integrandu na súčet alebo rozdiel.
• Integrácia pomocou zmeny premennej (substitúcia).
• Integrácia po častiach.

Aplikácia integrálu:

• Matematika
• Výpočty hodnôt S.
• Dĺžka oblúka krivky.
• V telesá na S rovnobežné rezy.
• V telesá revolúcie atď.

• fyzika
• Práca Premenlivá sila.
• S - (cesta) pohybu.
• Výpočet hmotnosti.
• Výpočet momentu zotrvačnosti priamky, kružnice, valca.
• Výpočet súradníc ťažiska.
• Množstvo tepla atď.

Ministerstvo školstva Saratovského regiónu

Štátny autonómny profesionál vzdelávacia inštitúcia Saratovský región "Engels Polytechnic"

APLIKÁCIA DERIVÁTU V RÔZNYCH VEDECKÝCH OBLASTIACH

Vykonané: Sarkulova Nurgulya Sergejevna

študent skupiny KShI-216/15

(dizajn, modelovanie a

technológia šitia)

Vedecký poradca:

Verbitskaja Elena Vyacheslavovna

učiteľka matematiky GAPOU SO

"Engelsova polytechnika"

2016

Úvod

Úloha matematiky v rôznych oblastiach prírodných vied je veľmi veľká. Niet divu, že hovoria„Matematika je kráľovnou vied, jej fyzika pravá ruka, chémia zostala.

Predmetom skúmania je derivát.

Hlavným cieľom je ukázať význam derivácie nielen v matematike, ale aj v iných vedách, jej význam v modernom živote.

Diferenciálny počet je opis sveta okolo nás vytvorený matematickým jazykom. Derivát nám pomáha úspešne riešiť nielen matematické problémy, ale aj praktické úlohy v rôznych oblastiach vedy a techniky.

Derivácia funkcie sa používa všade tam, kde dochádza k nerovnomernému toku procesu: je to nerovnomerný mechanický pohyb a striedavý prúd, chemické reakcie a rádioaktívny rozpad hmoty atď.

Kľúčové a tematické otázky tejto eseje:

1. História vzniku derivátu.

2. Prečo študovať derivácie funkcií?

3. Kde sa používajú deriváty?

4. Aplikácia derivátov vo fyzike, chémii, biológii a iných vedách.

5. Závery

Rozhodol som sa napísať prácu na tému „Aplikácia derivácie v rôznych oblastiach vedy“, pretože si myslím, že táto téma je veľmi zaujímavá, užitočná a relevantná.

Vo svojej práci budem hovoriť o aplikácii diferenciácie v rôznych oblastiach vedy, ako je chémia, fyzika, biológia, geografia atď. Všetky vedy sú predsa neoddeliteľne spojené, čo je veľmi dobre vidieť na príklade témy zvažujem.

Aplikácia derivátu v rôznych oblastiach vedy

Z kurzu algebry na strednej škole to už vieme derivát je hranica pomeru prírastku funkcie k prírastku jej argumentu, pretože prírastok argumentu má tendenciu k nule, ak takáto hranica existuje.

Akcia hľadania derivácie sa nazýva jej diferenciácia a funkcia, ktorá má deriváciu v bode x, sa v tomto bode nazýva diferencovateľná. Funkcia, ktorá je diferencovateľná v každom bode intervalu, sa nazýva diferencovateľná na tomto intervale.

Pocta objaviť základné zákony matematickej analýzy patrí anglickému fyzikovi a matematikovi Isaacovi Newtonovi a nemeckému matematikovi, fyzikovi, filozofovi Leibnizovi.

Newton predstavil pojem derivát, študoval zákony mechaniky, čím odhalil jeho mechanický význam.

Fyzikálny význam derivácie: derivácia funkcier= f(X) v bode X 0 je rýchlosť zmeny funkcief(X) v bode X 0 .

Leibniz prišiel ku konceptu derivácie vyriešením problému nakreslenia dotyčnice k derivačnej priamke, čím vysvetlil jej geometrický význam.

Geometrický význam derivácie je, že derivácia funguje v bodeX 0 rovná sklonu dotyčnice ku grafu funkcie nakreslenej v bode s osouX 0 .

Pojem derivácia a moderná notáciar" , f„Zaviedol ho J. Lagrange v roku 1797.

Ruský matematik z 19. storočia Panfuty Ľvovič Čebyšev povedal, že „tie metódy vedy, ktoré umožňujú riešiť problém spoločný pre všetkých praktické činnostičloveka, napríklad ako naložiť so svojimi prostriedkami, aby dosiahol čo najväčší úžitok.

Zástupcovia rôznych špecialít sa v súčasnosti musia zaoberať týmito úlohami:

Procesní inžinieri sa snažia organizovať výrobu tak, aby sa vyrobilo čo najviac produktov;

Dizajnéri sa snažia vyvinúť zariadenie pre vesmírna loď takže hmotnosť zariadenia je najmenšia;

Ekonómovia sa snažia naplánovať prepojenia medzi závodom a zdrojmi surovín tak, aby náklady na dopravu boli minimálne.

Pri štúdiu akejkoľvek témy majú študenti otázku: „Prečo to potrebujeme? Ak odpoveď uspokojí zvedavosť, môžeme hovoriť o záujme študentov. Odpoveď na tému „Derivácia“ možno získať tak, že budeme vedieť, kde sa používajú derivácie funkcií.

Na zodpovedanie tejto otázky môžeme uviesť niektoré disciplíny a ich sekcie, v ktorých sa deriváty používajú.

Derivát v algebre:

1. Tangenta ku grafu funkcie

Graf dotyčnice k funkciif, diferencovateľné na x o , je priamka prechádzajúca bodom (x o ; f(x o )) a má sklonf“(x o).

y= f(x o) + f′(x o) (x - x o)

2. Vyhľadajte intervaly rastúcich a klesajúcich funkcií

Funkciay=f(x) sa počas intervalu zvyšujeX , ak pre nejaké Anerovnosť. Inými slovami - väčšiu hodnotu argument zodpovedá väčšej hodnote funkcie.

Funkciay=f(x) počas intervalu klesáX , ak pre nejaké Anerovnosť. Inými slovami, väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.

3. Hľadanie extrémnych bodov funkcie

Bod volalmaximálny bod funkciey=f(x) ak pre všetkýchX . Zavolá sa hodnota funkcie v maximálnom bodemaximálna funkcia a označujú.

Bod volalminimálny bod funkciey=f(x) ak pre všetkýchX zo svojho okolia nerovnosť. Zavolá sa hodnota funkcie v minimálnom bodefunkčné minimum a označujú.

Pod susedstvom bodu pochopiť interval, kde je dostatočne malé kladné číslo.

Minimálny a maximálny počet bodov sa nazývaextrémne body , a volajú sa funkčné hodnoty zodpovedajúce extrémnym bodomfunkčné extrémy .

4. Hľadajte intervaly konvexnosti a konkávnosti funkcie

Graf funkcií, je na tomto intervalekonvexné , neleží vyššie ako ktorákoľvek z jeho dotyčníc (obr. 1).

Graf funkcií, diferencovateľné na intervale, je na tomto intervalekonkávne , ak je graf tejto funkcie v intervale neleží nižšie ako ktorákoľvek z jeho dotyčníc (obr. 2).

Inflexný bod funkčného grafu sa nazýva bod oddeľujúci intervaly konvexnosti a konkávnosti.

5. Nájdenie inflexných bodov funkcie

Derivát vo fyzike:

1. Rýchlosť ako derivát cesty

2. Zrýchlenie ako derivácia rýchlostia =

3. Rýchlosť rozpadu rádioaktívnych prvkov 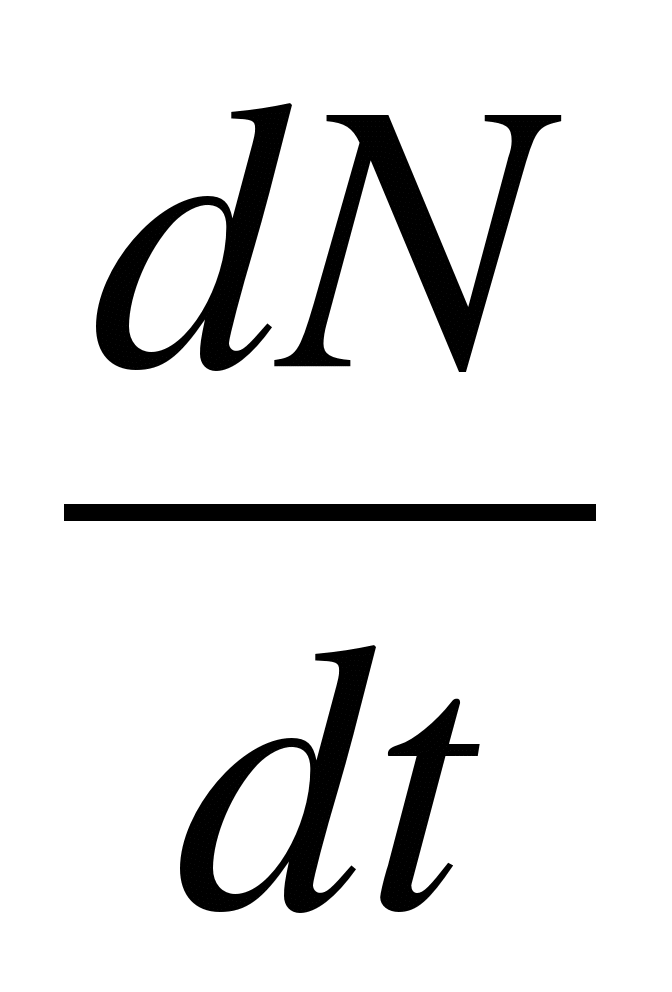= - λN

A tiež vo fyzike sa derivácia používa na výpočet:

Bodové rýchlosti materiálu

Okamžitá rýchlosť ako fyzikálny význam derivátu

Okamžitý striedavý prúd

Okamžitá hodnota EMF elektromagnetickej indukcie

Maximálny výkon

Derivát v chémii:

A v chémii našiel diferenciálny počet široké uplatnenie na zostavovanie matematických modelov chemických reakcií a následný popis ich vlastností.

Derivát v chémii sa používa na určenie veľmi dôležitej veci - rýchlosti chemickej reakcie, jedného z rozhodujúcich faktorov, ktorý treba brať do úvahy v mnohých oblastiach vedeckej a priemyselnej činnosti.. V(t) = p'(t)

množstvo

in-va naraz t 0

p = p(t 0 )

Funkcia

Časový interval

∆t = t – t 0

Prírastok argumentu

Zmena množstva

∆p=p(t 0 + ∆t) – p(t 0 )

Prírastok funkcie

Priemerná rýchlosť chemickej reakcie

∆p/∆t

Pomer prírastku funkcie k prírastku argumentu

Deriváty v biológii:

Populácia je súbor jedincov daného druhu, ktorí zaberajú určitú oblasť územia v rámci druhu, voľne sa navzájom krížia a čiastočne alebo úplne izolujú od iných populácií a je tiež základnou jednotkou evolúcie. .

P \u003d x“ (t)

Derivát v geografii:

1. Niektoré významy v seizmografii

2. Vlastnosti elektromagnetického poľa zeme

3. Rádioaktivita jadrových geofyzikálnych parametrov

4. Mnoho významov v ekonomickej geografii

5. Odvoďte vzorec na výpočet počtu obyvateľov v území v čase t.

y'= do y

Myšlienka sociologického modelu Thomasa Malthusa je taká, že rast populácie je úmerný počtu obyvateľov v danom čase t až N(t). Malthusov model dobre fungoval na opis populácie USA v rokoch 1790 až 1860. Tento model už vo väčšine krajín neplatí.

Derivát v elektrotechnike:

V našich domovoch, v doprave, v továrňach: elektrický prúd funguje všade. Pod elektrickým prúdom rozumieme usmernený pohyb voľných elektricky nabitých častíc.

Kvantitatívna charakteristika elektrického prúdu je sila prúdu.

V obvode elektrického prúdu sa elektrický náboj v priebehu času mení podľa zákona q=q (t). Prúd I je deriváciou náboja q vzhľadom na čas.

V elektrotechnike sa využíva najmä striedavá prevádzka.

Elektrický prúd, ktorý sa mení s časom, sa nazýva striedavý prúd. Obvod striedavého prúdu môže obsahovať rôzne prvky: ohrievače, cievky, kondenzátory.

Výroba striedavého elektrického prúdu je založená na zákone elektromagnetickej indukcie, ktorého formulácia obsahuje derivát magnetického toku.

Derivát v ekonómii:

Ekonomika je základom života a diferenciálny počet, prístroj na ekonomickú analýzu, v ňom zaujíma dôležité miesto. Základnou úlohou ekonomickej analýzy je študovať vzťahy ekonomických veličín vo forme funkcií.

Derivát v ekonómii rieši dôležité otázky:

1. Akým smerom sa zmenia príjmy štátu zvýšením daní alebo zavedením ciel?

2. Zvýšia sa alebo znížia sa príjmy spoločnosti s rastom ceny jej produktov?

Na vyriešenie týchto otázok je potrebné zostrojiť spojovacie funkcie vstupných premenných, ktoré sú následne študované metódami diferenciálneho počtu.

Taktiež pomocou extrému funkcie (derivátu) v ekonomike môžete nájsť najvyššiu produktivitu práce, maximálny zisk, maximálny výkon a minimálne náklady.

VÝKON: derivát sa úspešne používa pri riešení rôznych aplikovaných problémov vo vede, technike a živote

Ako vidno z vyššie uvedeného, ​​využitie derivácie funkcie je veľmi rôznorodé, a to nielen pri štúdiu matematiky, ale aj v iných odboroch. Preto môžeme konštatovať, že štúdium témy: „Derivácia funkcie“ bude mať svoje uplatnenie aj v iných témach a predmetoch.

Presvedčili sme sa o dôležitosti naštudovania témy „Derivácia“, jej úlohe pri štúdiu procesov vedy a techniky, možnosti projektovania podľa skutočné udalosti matematické modely a riešiť dôležité problémy.

“Hudba môže povzniesť alebo upokojiť dušu,
Maľovanie lahodí oku,
Poézia - prebudiť pocity,
Filozofia - uspokojiť potreby mysle,
Inžinierstvo má zlepšiť materiálnu stránku života ľudí,
ALEmatematika môže dosiahnuť všetky tieto ciele.“

Tak povedal americký matematikMaurice Kline.

Bibliografia:

1. Bogomolov N.V., Samoylenko I.I. Matematika. - M.: Yurayt, 2015.

2. V. P. Grigoriev a Yu. A. Dubinsky, Základy vyššej matematiky. - M.: Akadémia, 2014.

3. Bavrin I.I. Základy vyššej matematiky. - M.: stredná škola, 2013.

4. Bogomolov N.V. Workshopy matematiky. - M.: Vysoká škola, 2013.

5. Bogomolov N.V. Zbierka úloh z matematiky. - M.: Drop, 2013.

6. Rybnikov K.A. Dejiny matematiky, Moskovská univerzita, M, 1960.

7. Vinogradov Yu.N., Gomola A.I., Potapov V.I., Sokolova E.V. – M.:Vydavateľské centrum "Akadémia", 2010

8 . Bašmakov M.I. Matematika: algebra a začiatky matematickej analýzy, geometria. - M.: Vydavateľské centrum "Akadémia", 2016

Pravidelné zdroje:

Noviny a časopisy: "Matematika", " Verejná lekcia»

Používanie internetových zdrojov, digitálnych knižníc:

www:egetutor.ru

matematika-na5.norod.ru

Späť dopredu

Pozor! Ukážka snímky slúži len na informačné účely a nemusí predstavovať celý rozsah prezentácie. Ak vás táto práca zaujala, stiahnite si plnú verziu.

Typ lekcie: integrovaný.

Účel lekcie:študovať niektoré aspekty aplikácie derivátu v rôznych oblastiach fyziky, chémie, biológie.

Úlohy: rozširovanie obzorov a poznávacia činnosť žiakov, rozvoj logické myslenie a schopnosť uplatniť svoje vedomosti.

Technická podpora: interaktívna tabuľa; počítač a disk.

POČAS VYUČOVANIA

I. Organizačný moment

II. Stanovenie cieľa lekcie

- Chcel by som viesť lekciu pod heslom Alexeja Nikolajeviča Krylova, sovietskeho matematika a staviteľa lodí: "Teória bez praxe je mŕtva alebo zbytočná, prax bez teórie je nemožná alebo zhubná."

Zopakujme si základné pojmy a odpovedzme na otázky:

Aká je základná definícia derivátu?
– Čo viete o derivácii (vlastnosti, vety)?
– Poznáte nejaké príklady odvodených úloh z fyziky, matematiky a biológie?

Úvaha o základnej definícii derivátu a jeho odôvodnení (odpoveď na prvú otázku):

Derivát je jedným zo základných pojmov matematiky. Schopnosť riešiť problémy pomocou derivácie vyžaduje dobré znalosti teoretický materiál schopnosť vykonávať výskum v rôznych situáciách.

Preto si dnes v lekcii upevníme a systematizujeme získané poznatky, zvážime a zhodnotíme prácu každej skupiny a na príklade niektorých úloh si ukážeme, ako použiť deriváciu na riešenie iných problémov a neštandardných úloh pomocou derivát.

III. Vysvetlenie nového materiálu

1. Okamžitý výkon je odvodením práce s ohľadom na čas:

W = limit ∆A/∆t ∆A – zmena zamestnania.

2. Ak sa teleso otáča okolo osi, potom je uhol natočenia funkciou času t
Potom je uhlová rýchlosť:

W = lim Δφ/Δt = φ׳(t) Δ t → 0

3. Prúdová sila je odvodená Ι = lim Δg/Δt = g′, kde g- kladný elektrický náboj prenesený cez prierez vodiča v čase Δt.

4. Nechajte ∆Q je množstvo tepla potrebné na zmenu teploty Δtčas teda lim ΔQ/Δt = Q′ = C –špecifické teplo.

5. Problém rýchlosti chemickej reakcie

m(t) – m(t0) – množstvo látky, ktoré v priebehu času reaguje t0 predtým t

V= lim ∆m/∆t = m ∆t → 0

6. Nech m je hmotnosť rádioaktívnej látky. Rýchlosť rádioaktívneho rozpadu: V = lim ∆m/∆t = m׳(t) ∆t→0

V diferencovanej forme má zákon rádioaktívneho rozpadu tvar: dN/dt = – λN, kde N je počet jadier, ktoré sa časom nerozpadli t.

Integráciou tohto výrazu dostaneme: dN/N = – λdt ∫dN/N = – λ∫dt lnN = – λt + c, c = konšt. pri t = 0 počet rádioaktívnych jadier N = N0, teda máme: log N0 = konštanta, V dôsledku toho

n N = – λt + ln N0.

Zosilnením tohto výrazu dostaneme:

je zákon rádioaktívneho rozpadu, kde N0 je počet jadier naraz to = 0, N je počet jadier, ktoré sa časom nerozpadli t.

7. Podľa Newtonovej rovnice prenosu tepla rýchlosť tepelného toku dQ/dt je priamo úmerná ploche okna S a teplotnému rozdielu ΔT medzi vnútorným a vonkajším sklom a nepriamo úmerná jeho hrúbke d:

dQ/dt = A S/d ∆T

8. Fenomén difúzie je proces nastolenia rovnovážneho rozdelenia

V rámci fáz koncentrácie. Difúzia ide do strany, čím sa vyrovnávajú koncentrácie.

m = D ∆c/∆x c – koncentrácie
m = D c x x x - koordinovať, D- difúzny koeficient

Fickov zákon:

9. Bolo známe, že elektrické pole budí buď elektrické náboje, alebo magnetické pole, ktoré má jediný zdroj – elektrický prúd. James Clark Maxwell zaviedol jeden dodatok k zákonom elektromagnetizmu objaveným pred ním: magnetické pole vzniká aj vtedy elektrické pole. Na prvý pohľad malá novela mala veľkolepé dôsledky: objavil sa úplne nový fyzický objekt, aj keď na špičke pera, elektromagnetická vlna. Maxwell majstrovsky vlastnil, na rozdiel od Faradaya, ktorý sa zdal možným jeho existencie, odvodil rovnicu pre elektrické pole:

∂E/∂x = M∂B/Mo ∂t Mo = konštantná t

Zmena elektrického poľa spôsobuje výskyt magnetického poľa v akomkoľvek bode priestoru, inými slovami, rýchlosť zmeny elektrického poľa určuje veľkosť magnetického poľa. Pod veľkým elektrickým prúdom - veľké magnetické pole.

IV. Konsolidácia študovaného

– Študovali sme derivát a jeho vlastnosti. Rád by som si prečítal Gilbertov filozofický výrok: „Každý človek má určitý pohľad. Keď sa tento horizont zúži na nekonečne malý, zmení sa na bod. Potom človek povie, že toto je jeho uhol pohľadu.
Skúsme zmerať uhol pohľadu na aplikáciu derivácie!

Zápletka "Leaf"(aplikácia derivátu v biológii, fyzike, živote)

Považujte pád za nerovnomerný pohyb v závislosti od času.

Takže: S = S(t) V = S′(t) = x′(t), a = V′(t) = S″(t)

(Teoretický prehľad: mechanický význam derivátu).

1. Riešenie problémov

Riešte problémy po svojom.

2. F = ma F = mV′ F = mS″

Napíšme Portonov zákon II a s prihliadnutím na mechanický význam derivácie ho prepíšeme do tvaru: F = mV′ F = mS″

Dej filmu "Wolves, Gophers"

Vráťme sa k rovniciach: Zvážte diferenciálne rovnice exponenciálneho rastu a poklesu: F = ma F = mV" F = mS""
Riešenie mnohých problémov fyziky, technickej biológie a spoločenských vied sa redukuje na problém hľadania funkcií f"(x) = kf(x), splnenie diferenciálnej rovnice, kde k = konšt .

Ľudský vzorec

Človek je toľkokrát väčší ako atóm, ako je menší ako hviezda:

Z toho teda vyplýva
Toto je vzorec, ktorý určuje miesto človeka vo vesmíre. V súlade s ním rozmery osoby predstavujú priemerný pomer hviezdy a atómu.

Lekciu by som rád ukončil slovami Lobačevského: „Neexistuje jediná oblasť matematiky, bez ohľadu na to, aká abstraktná môže byť, ktorá sa jedného dňa nebude dať použiť na javy skutočného sveta.

V. Riešenie čísel z kolekcie:

Nezávislé riešenie problémov na tabuli, kolektívna analýza riešení problémov:

№ 1 Nájdite rýchlosť hmotného bodu na konci 3. sekundy, ak je pohyb bodu daný rovnicou s = t^2 –11t + 30.

№ 2 Bod sa pohybuje priamočiaro podľa zákona s = 6t – t^2. V akom bode bude jeho rýchlosť nulová?

№ 3 Dve telesá sa pohybujú po priamke: jedno podľa zákona s \u003d t^3 - t^2 - 27t, druhé - podľa zákona s \u003d t^2 + 1. Určte okamih, kedy budú rýchlosti týchto telá sú si rovné.

№ 4 Pre automobil pohybujúci sa rýchlosťou 30 m/s je brzdná dráha určená vzorcom s(t) =30t-16t^2, kde s(t) je vzdialenosť v metroch, t je brzdný čas v sekundách. . Ako dlho trvá spomalenie, kým sa auto úplne nezastaví? Akú vzdialenosť prejde auto od začiatku brzdenia až po úplné zastavenie?

№5 Teleso s hmotnosťou 8 kg sa pohybuje po priamke podľa zákona s = 2t^2+ 3t - 1. Nájdite kinetickú energiu telesa (mv^2/2) 3 sekundy po začatí pohybu.

Riešenie: Nájdite rýchlosť tela kedykoľvek:
V=ds/dt=4t+3
Vypočítajte rýchlosť telesa v čase t = 3:
Vt \u003d 3 \u003d 4 * 3 + 3 \u003d 15 (m / s).
Určme kinetickú energiu telesa v čase t = 3:
mv2/2 = 8 - 15^2/2 = 900 (J).

№6 Nájdite kinetickú energiu telesa 4 s po začatí pohybu, ak jeho hmotnosť je 25 kg a pohybový zákon je s = 3t^2-1.

№7 Teleso s hmotnosťou 30 kg sa pohybuje priamočiaro podľa zákona s = 4t^2 + t. Dokážte, že pohyb telesa nastáva pôsobením konštantnej sily.
Riešenie: Máme s" = 8t + 1, s" = 8. Preto a(t) = 8 (m/s^2), teda pri danom pohybovom zákone sa teleso pohybuje s konštantným zrýchlením 8 m. /s^2. Ďalej, keďže hmotnosť telesa je konštantná (30 kg), potom podľa druhého Newtonovho zákona je konštantnou hodnotou aj sila, ktorá naň pôsobí F = ma = 30 * 8 = 240 (H).

№8 Teleso s hmotnosťou 3 kg sa pohybuje po priamke podľa zákona s(t) = t^3 - 3t^2 + 2. Nájdite silu pôsobiacu na teleso v čase t = 4s.

№9 Hmotný bod sa pohybuje podľa zákona s = 2t^3 – 6t^2 + 4t. Nájdite jeho zrýchlenie na konci 3. sekundy.

VI. Aplikácia derivácie v matematike:

Derivácia v matematike ukazuje číselné vyjadrenie stupňa zmeny veličiny nachádzajúcej sa v rovnakom bode pod vplyvom rôznych podmienok.

Odvodený vzorec pochádza z 15. storočia. Veľký taliansky matematik Tartaglia, zvažujúci a rozvíjajúci otázku - do akej miery závisí dosah strely od sklonu pištole - ju používa vo svojich spisoch.

Odvodený vzorec sa často nachádza v dielach slávnych matematikov 17. storočia. Používajú ho Newton a Leibniz.

Známy vedec Galileo Galilei venuje úlohu derivátu v matematike celé pojednanie. Potom sa derivát a rôzne prezentácie s jeho aplikáciou začali nachádzať v dielach Descarta, francúzskeho matematika Robervala a Angličana Gregoryho. Veľký príspevok k štúdiu derivátu mali také mysle ako Lopital, Bernoulli, Langrange a ďalší.

1. Nakreslite a preskúmajte funkciu:

Riešenie tohto problému:

Chvíľka relaxu

VII. Aplikácia derivácie vo fyzike:

Pri štúdiu určitých procesov a javov často vzniká problém určiť rýchlosť týchto procesov. Jeho riešenie vedie ku konceptu derivácie, čo je základný koncept diferenciálneho počtu.

Metóda diferenciálneho počtu vznikla v 17. a 18. storočí. Mená dvoch veľkých matematikov I. Newtona a G.V. Leibniz.

Newton dospel k objavu diferenciálneho počtu pri riešení úloh o rýchlosti hmotného bodu v danom časovom okamihu (okamžitá rýchlosť).

Vo fyzike sa derivácia používa najmä na výpočet najväčšej resp najmenšie hodnoty akékoľvek množstvá.

Riešenie problémov:

№1 Potenciálna energia U pole častice, v ktorom je iná, presne tá istá častica, má tvar: U = a/r 2 – b/r, kde a A b sú kladné konštanty, r- vzdialenosť medzi časticami. Nájdite: a) hodnotu r0 zodpovedajúce rovnovážnej polohe častice; b) zistiť, či je táto situácia stabilná; v) Fmax hodnota sily príťažlivosti; d) zobrazujú približné grafy závislosti U(r) A F(r).

Riešenie tohto problému: Určiť r0 zodpovedajúcej rovnovážnej polohe častice, skúmame f = U(r) do krajnosti.

Použitie vzťahu medzi potenciálnou energiou poľa

U A F, potom F = -dU/dr, dostaneme F = – dU/dr = – (2a/r3+ b/r2) = 0; kde r = r0; 2a/r3 = b/r2 => ro = 2a/b; Stabilná alebo nestabilná rovnováha je určená znamienkom druhej derivácie:
d2U/dr02= dF/dr0 = – 6a/r02 + 2b/r03 = – 6a/(2a/b)4 + 2b/(2a/b)3 = (– b4/8a3)< 0 ;
rovnováha je stabilná.

Na určenie Fmax príťažlivosť, skúmam funkciu pre extrémy: F = 2a/r3 - b/r2;
dF/dr = –6a/r4 + 2b/r3 = 0; pri r = r1 = 3a/b; nahrádzanie, chápem Fmax = 2a/r31 - b/r31 = – b3/27a2; U(r) = 0; pri r = a/b; U(r)min pri r = 2, a/b = r0;F = 0; F(r)max pri r = r1 = 3a/b;
odpoveď: F(r)max pri r = r1 = 3a/b;

№2 Obvod s vonkajším odporom R = 0,9 ohm napájaný batériou k = 36 identické zdroje, z ktorých každý má emf E=2 IN a vnútorný odpor r0 = 0,4 ohmu. Vrátane batérie n skupiny zapojené paralelne a každá z nich obsahuje m batérie zapojené do série. V akých hodnotách m, n dostane maximum J vo vonkajšom R.

Riešenie tohto problému:

Keď sú batérie zapojené do série E gr = m* E ; rgr = r0*m;
a s paralelným zapojením toho istého rbat = r0m/n; E baht = m* E,
Ohmov zákon J = m E /(R+ r0m/n) = m E n/(nR + r0m)
Pretože k je celkový počet batérií, potom k = mn;
J=k E /(nR + r0m) = k E /(nR + kr0/n);
Ak chcete nájsť podmienku, za ktorej J prúd v obvode maximum preskúmať funkciu J = J(n) extrém tak, že vezmeme deriváciu vzhľadom na n a prirovnáme ju k nule.
J'n - (k E (R - kr0/n2))/ (nR + kr0/n)2 = 0;
n2 = kr/R
n = √kr/R = √3,6*0,4/0,9 = 4;
m = k/n = 36/4 = 9;
kde Jmax = k E / (nR + mr0) \u003d 36 * 2 / (4 * 0,9 + 9 * 0,4) \u003d 10 A;

odpoveď: n = 4, m = 9.

№3 Hromadná platforma M sa pôsobením konštantnej sily začne pohybovať doprava F. Piesok sa na ňu naleje zo stacionárneho bunkra. Rýchlosť nakladania je konštantná a rovná µ kg/s. Pri zanedbaní trenia nájdite závislosť od času zrýchlenia a plošiny počas nakladania. Určte zrýchlenie a1 plošina v prípade, že sa piesok nesype na plošinu, ale z naplnenej sa vysype cez otvor v jej dne konštantnou rýchlosťou µ kg/s.

Riešenie tohto problému: Najprv zvážte prípad, keď sa na plošinu naleje piesok
Pohyb systému platforma-piesok možno opísať pomocou druhého Newtonovho zákona:
dP/dt = FΣ
P je hybnosť systému platforma-piesok, FΣ je sila pôsobiaca na systém platforma-piesok.
Ak cez p označujú hybnosť platformy, potom môžeme napísať: dp/dt = F
Nájdite zmenu hybnosti platformy za nekonečne malý časový interval Δ t: Δ p = (M + u(t+ Δ t)) (u +Δ u) – (M + ut)u = FΔ t;
kde u- rýchlosť platformy.
Otvorením zátvoriek a vykonaním redukcií dostaneme:
Dp = uΔ t+MΔ u+ Δ µut +Δ µuΔ t = FΔ t
Vydeľte Δt a prejdite na limitu Δ t→ 0
Mdu/dt + utdu/dt + uu= F alebo d[(M + ut)u]/dt = F
Táto rovnica môže byť integrovaná za predpokladu, že počiatočná rýchlosť platformy je nulová: (M + ut)u = Ft.
V dôsledku toho: u = Ft/(M + µt)
Potom zrýchlenie platformy: a = du/dt = (F(M + µt) – Ftµ)/(M + µt) 2 = FM / (M + µt) 2

Zvážte prípad, keď sa piesok vysype z naplnenej plošiny.
Zmena hybnosti v krátkom časovom období:
Δ p = (M – u(t+Δ t)) (u+Δ u) +Δ µtu – (M – µt)u = FΔ t
Termín Δ µtu je hybnosť množstva piesku, ktoré sa vysypalo z plošiny za čas Δ t. potom:
Δ p = MΔ u-µtΔ u-Δ µtΔ u=FΔ t
Deliť Δ t a prejsť na limitu Δ t→ 0
(M – µt)du/dt = F
Alebo a1= du/dt= F/(M – µt)

odpoveď: a = FM / (M + µt)2, a1= F/(M - µt)

VIII.Samostatná práca:

Nájdite deriváty funkcií:

Priamka y \u003d 2x je dotyčnicou funkcie: y \u003d x 3 + 5x 2 + 9x + 3. Nájdite úsečku bodu dotyku.

IX. Zhrnutie lekcie:

- Aké boli témy hodiny?
- Čo si sa naučil v triede?
Aké teoretické fakty boli zhrnuté v lekcii?
– Ktoré úlohy boli považované za najťažšie? prečo?

Bibliografia:

1. Amelkin V.V., Sadovský A.P. Matematické modely a diferenciálne rovnice. - Minsk: Vyššia škola, 1982. - 272 s.
2. Amelkin V.V. Diferenciálne rovnice v aplikáciách. M.: Veda. Hlavné vydanie fyzikálnej a matematickej literatúry, 1987. - 160s.
3. Erugin N.P. Kniha na čítanie o všeobecnom priebehu diferenciálnych rovníc. - Minsk: Veda a technika, 1979. - 744 s.
4. .Časopis "Potenciál" November 2007 №11
5. "Algebra a začiatky analýzy" 11. ročník S.M. Nikolsky, M.K. Potapov a ďalší.
6. "Algebra a matematická analýza" N.Ya. Vilenkin a ďalší.
7. "Matematika" V.T. Lisichkin, I.L. Soloveichik, 1991

Úloha. Nákladová funkcia má tvar a produkčný príjem X Jednotky tovaru sú definované takto:

Určite optimálnu výstupnú hodnotu pre výrobcu x0.

Riešenie:

Zisk P(x) =D(X) - C(x), kde D(X) - príjem z výroby X jednotky produktu.

Funkcia zisku vyzerá takto:

Nájdite deriváciu funkcie zisku:

samozrejme, P "(x) > 0 pri X< 100 tak najvyššia hodnota v segmente sú zisky R(100) = 399 900. Teraz nájdime najväčšiu hodnotu zisku v intervale (100; + ∞). Je tu jeden kritický bod x= 200. V rovnakom čase P "(x)> 0 pri 100< X < 200 и R" (X)< 0 pri X> 200, t.j. x= 200 - maximálna hodnota P(x) na intervale (100; + ∞).

R(200) = 419 900 > R(100), takže X veľkoobchod = 200 (jednotka).

Úloha. Cementáreň vyrobí X ton cementu denne. Stavebnej firme musí podľa zmluvy dodať denne minimálne 20 ton cementu. Výrobná kapacita závodu je taká, že produkcia cementu nemôže presiahnuť 90 ton za deň.

Určte, pri akom objeme výroby budú jednotkové náklady najväčšie (najmenšie), ak má nákladová funkcia tvar:

K=-x3+98x2+200x. Jednotkové náklady budú K/x=-x2+98x+200

Riešenie:

Problém je redukovaný na nájdenie najväčších a najmenších hodnôt funkcie

y= - x2+98x+200. Medzi.

DIV_ADBLOCK1021">

6 Aplikácia derivátu v medicíne

Aplikácia diferenciálneho počtu v medicíne sa redukuje na výpočet rýchlosti. Napríklad rýchlosti regeneračných reakcií a rýchlosti relaxačného procesu.

Reakcia tela na podaný liek môže byť vyjadrená zvýšením krvného tlaku, zmenou telesnej teploty, zmenou pulzu alebo inými fyziologickými ukazovateľmi. Stupeň reakcie závisí od predpísaného lieku, jeho dávky. Pomocou derivátu môžete vypočítať, pri akej dávke lieku je reakcia tela maximálna. Pomocou druhej derivácie je možné určiť podmienky, za ktorých je rýchlosť procesu najcitlivejšia na akékoľvek vplyvy

Úloha Predstierajme to X označuje dávku predpísaného lieku, pri je funkciou stupňa reakcie. y=f(x)=x²(a-x), kde ale je nejaká pozitívna konštanta. V akej hodnote X maximálna odozva?

Riešenie:

https://pandia.ru/text/80/244/images/image137_6.gif" width="116" height="24">. Potom pomocou ..gif" width="49" height="42"> - úroveň dávky, ktorá poskytuje maximálnu odozvu.

Inflexné body sú dôležité v biochémii, pretože definujú podmienky, za ktorých je určitá veličina, ako napríklad rýchlosť procesu, najviac (alebo najmenej) citlivá na akékoľvek vplyvy.

Úloha. V dôsledku výraznej straty krvi sa obsah železa v krvi znížil o 210 mg. Nedostatok železa v dôsledku jeho obnovy v priebehu času t klesá podľa zákona mg (t - deň). Nájdite závislosť rýchlosti obnovy železa v krvi od času. Vypočítajte túto rýchlosť v tejto chvíli t=0 a po 7 dňoch.

Riešenie:

Rýchlosť regenerácie železa:

https://pandia.ru/text/80/244/images/image144_5.gif" width="33" height="18"> miera obnovy je 30 mg/deň. Po 7 dňoch je miera obnovy 11,1 mg /deň dní:

Relaxačný proces je proces návratu systému do stavu stabilnej rovnováhy, z ktorej bol prevzatý. V mnohých prípadoch (najmä pri jednorazovej expozícii) je tento proces opísaný exponenciálnou rovnicou. Jeho fyzikálny význam je: - je to čas, počas ktorého dôjde k počiatočnej odchýlke výskumnej činnosti" href="/text/category/nauchno_issledovatelmzskaya_deyatelmznostmz/" rel. ="bookmark">výskumná a výrobná činnosť. Napríklad procesní inžinieri pri zisťovaní účinnosti chemickej výroby, chemici vyvíjajúci lieky pre medicínu a poľnohospodárstvo, ale aj lekári a agronómovia, ktorí tieto lieky používajú na liečbu ľudí a aplikujú ich do pôdy. Niektoré reakcie sú takmer okamžité, zatiaľ čo iné sú veľmi pomalé. IN skutočný život na riešenie výrobných problémov v medicínskom, poľnohospodárskom a chemickom priemysle je dôležité poznať reakčné rýchlosti chemikálií.

Nechajte funkciu m=m(t), kde m- množstvo látky, ktoré naraz vstúpilo do chemickej reakcie t. Časový prírastok Δt bude zodpovedať prírastku ∆m množstvá m. Postoj ∆m/∆t je priemerná rýchlosť chemickej reakcie za určité časové obdobie Δt. Hranica tohto pomeru pri snažení Δt k nule je rýchlosť chemickej reakcie v danom čase.

Úloha. Vzťah medzi hmotnosťou x látky získanej ako výsledok nejakej chemickej reakcie a časom t vyjadrené rovnicou https://pandia.ru/text/80/244/images/image151_5.gif" width="283" height="30 src=">

Úloha. Koncentrácia roztoku sa v čase mení podľa zákona: . Nájdite rýchlosť rozpúšťania.

Riešenie:

Rýchlosť rozpúšťania sa vypočíta pomocou derivátu:

https://pandia.ru/text/80/244/images/image154_4.gif" width="139" height="42 src=">. Získajte vzorec pre mieru rastu populácie.

Riešenie:

Úloha. Závislosť dennej dojivosti r v litroch od veku kráv X v rokoch je určená rovnicou , kde x>2. Nájdite vek dojníc, v ktorom bude denná dojivosť najvyššia.

Riešenie:

https://pandia.ru/text/80/244/images/image161_4.gif" width="77" height="23 src=">

(roky) - maximálny bod, vek dojníc, v ktorom bude denná dojivosť najväčšia.

Záver

V tomto článku sa zaoberáme jedným z najdôležitejších konceptov matematickej analýzy - deriváciou funkcie z hľadiska jej praktické uplatnenie. S pomocou derivátu môžete vyriešiť širokú škálu problémov týkajúcich sa akejkoľvek oblasti. ľudská aktivita. Najmä pomocou derivácií je možné detailne študovať funkcie, presnejšie zostavovať ich grafy, riešiť rovnice a nerovnice, dokazovať identity a nerovnosti a nájsť najväčšie a najmenšie hodnoty veličín.

Pre všetky vyššie uvedené oblasti použitia derivátu bolo vybratých asi dvesto problémov a zhrnutých do zbierky. Každá časť zborníka začína stručným zhrnutím teoretických základov, obsahuje typické úlohy s riešeniami a zostavami cvičení na nezávislé rozhodnutie. Tieto úlohy rozširujú obzory a zvyšujú záujem o derivát. Môžu byť zaujímavé a užitočné pre študentov, ktorí majú radi matematiku.

Literatúra

1. Bogomolove úlohy z matematiky: učebnica pre vysoké školy. – M.: Drop, 2005.

2. Bogomolov: učebnica. pre vysoké školy /, - M .: Drop, 2010.

3. Bogomolov. Didaktické úlohy: učebnica. príspevok na vysoké školy /, - M .: Drop, 2005.

4. Istomina: otázky a odpovede: učebnica. príspevok pre vysoké školy. - Rostov n / a: Phoenix, 2002.

5. Lisichkin: učebnica. príspevok pre technické školy /, - M.: Vyš. škola, 1991.

6. Nikolsky matematická analýza: učebnica. príspevok pre študentov. ssuzov.- M.: Drop, 2012.

7. Omelčenko: učebnica. príspevok na vysoké školy. - Rostov n / a: Phoenix, 2007.

8. Filimonova: učebnica. príspevok na vysoké školy. – Rostov n/a: Phoenix, 2013.