Descrizione della presentazione su singole diapositive:

1 diapositiva

Descrizione della diapositiva:

Argomento della lezione: applicazione della derivata in vari campi della conoscenza Insegnante di matematica MBOU "Scuola n. 74" Zagumenova Marina Vladimirovna

2 diapositive

Descrizione della diapositiva:

Scopo della lezione: apprendere le principali aree di applicazione del derivato in vari campi della scienza e della tecnologia; Considera, usando esempi di risoluzione di problemi pratici, come il derivato viene utilizzato in chimica, fisica, biologia, geografia ed economia.

3 diapositiva

Descrizione della diapositiva:

"Non esiste una singola area della matematica, per quanto astratta possa essere, che un giorno non sarà applicabile ai fenomeni del mondo reale". NI Lobachevskij

4 diapositive

Descrizione della diapositiva:

Regole di differenziazione Derivata di una somma A proposito di un fattore costante Derivata di un prodotto Derivata di una frazione Derivata di una funzione complessa (u+v)"= u" + v' (Cu)"=Cu' (uv)"=u"v +uv' (u/v)" =(u"v-uv")/v2 hꞌ(x)=gꞌ(f(x))f ꞌ(x)

5 diapositiva

Descrizione della diapositiva:

Derivata in fisica Problema. Il movimento della cabina durante la frenata è descritto dalla formula s(t) = 30t - 5t2, (s è lo spazio di arresto in metri, t è il tempo in secondi dall'inizio della frenata all'arresto completo della cabina). Trova per quanti secondi l'auto è in movimento dal momento in cui inizia a frenare fino a quando si ferma completamente. Qual è la distanza percorsa dall'auto dall'inizio della frenata fino all'arresto completo? Soluzione: poiché la velocità è la derivata prima del movimento nel tempo, allora v = S'(t) = 30 - 10t, perché in frenata la velocità è zero, quindi 0=30–10t; 10t=30; t=3(sec). Distanza di arresto S(t) = 30t - 5t2 = 30∙3-5∙32 = 90-45 = 45(m). Risposta: tempo di decelerazione 3s, spazio di frenata 45m.

6 diapositiva

Descrizione della diapositiva:

Questo è interessante Steamship "Chelyuskin" nel febbraio 1934 ha superato con successo l'intera rotta del mare settentrionale, ma in stretto di Bering era intrappolato nel ghiaccio. Il ghiaccio portò il Chelyuskin a nord e lo frantumò. Ecco una descrizione del disastro: "Il robusto metallo dello scafo non ha ceduto immediatamente", ha riferito alla radio il capo della spedizione, O.Yu. Schmidt. - Era visibile come il lastrone di ghiaccio fosse premuto sul lato e come i fogli di rivestimento sopra di esso si gonfiassero, piegandosi verso l'esterno. Il ghiaccio continuava la sua lenta ma irresistibile avanzata. Le lastre di ferro gonfie del fasciame dello scafo erano strappate alla giuntura. I rivetti volavano con una crepa. In un istante, il lato sinistro della nave è stato strappato dalla stiva di prua all'estremità poppiera del ponte ... "Perché è accaduto il disastro?

7 diapositiva

Descrizione della diapositiva:

La forza di pressione del ghiaccio Р è scomposta in due: F e R. R è perpendicolare alla tavola, F è diretta tangenzialmente. L'angolo tra P e R - α - l'angolo del lato rispetto alla verticale. Q è la forza di attrito del ghiaccio contro la tavola. Q = 0,2 R (0,2 è il coefficiente di attrito). Se Q< F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q >F, quindi l'attrito impedisce al lastrone di ghiaccio di scivolare e il ghiaccio può schiacciare e spingere la tavola. 0.2R< R tgα , tgα >0,2; Q< F, если α >1100. L'inclinazione delle fiancate della nave rispetto alla verticale di un angolo α > 1100 garantisce una navigazione sicura sul ghiaccio.

8 diapositiva

Descrizione della diapositiva:

Derivato in chimica Derivato in chimica viene utilizzato per determinare la velocità reazione chimica. Ciò è necessario per: ingegneri di processo nel determinare l'efficacia della produzione chimica, chimici che sviluppano farmaci per la medicina e agricoltura, così come i medici e gli agronomi che usano questi farmaci per curare le persone e per applicarli al suolo. Per risolvere i problemi di produzione nell'industria medica, agricola e chimica, è semplicemente necessario conoscere le velocità di reazione delle sostanze chimiche.

9 diapositiva

Descrizione della diapositiva:

Problema in chimica Sia data dalla dipendenza la quantità di una sostanza che è entrata in una reazione chimica: р(t) = t2/2 + 3t –3 (mol). Trova la velocità di una reazione chimica dopo 3 secondi. Riferimento: la velocità di una reazione chimica è la variazione della concentrazione di reagenti per unità di tempo o la derivata della concentrazione di reagenti rispetto al tempo (nel linguaggio della matematica, la concentrazione sarebbe una funzione e il tempo sarebbe un argomento )

10 diapositive

Descrizione della diapositiva:

Concetto di soluzione nel linguaggio della chimica Concetto di notazione nel linguaggio della matematica Quantità di sostanza al tempo t0 p = p(t0) Funzione Intervallo di tempo ∆t = t – t0 Incremento di argomento Variazione della quantità di sostanza ∆p = p(t0+ ∆ t) – p(t0) Incremento della funzione Velocità media di una reazione chimica ∆p/∆t Il rapporto tra l'incremento della funzione e l'incremento dell'argomento V (t) = p'(t)

11 diapositiva

Descrizione della diapositiva:

Derivato in biologia Problema in biologia: Sulla base della nota dipendenza della dimensione della popolazione x(t), determinare la crescita relativa al tempo t. Riferimento: Una popolazione è un insieme di individui di una data specie, che occupano una determinata area del territorio all'interno dell'area di distribuzione della specie, che si incrociano liberamente tra loro e parzialmente o completamente isolati da altre popolazioni, ed è anche un'unità elementare di evoluzione.

12 diapositiva

Descrizione della diapositiva:

Concetto di soluzione nel linguaggio della biologia Concetto di notazione nel linguaggio della matematica Numero al tempo t x = x(t) Funzione Intervallo di tempo ∆t = t – t0 Incremento dell'argomento Variazione della popolazione ∆x = x(t) – x(t0) Incremento della funzione Tasso di variazione della dimensione della popolazione ∆x/∆t Il rapporto tra l'incremento della funzione e l'incremento dell'argomento Crescita relativa in un dato momento lim∆x/∆t ∆t → 0 Derivata Р = x" ( t)

13 diapositiva

Descrizione della diapositiva:

14 diapositiva

Descrizione della diapositiva:

Derivato in geografia Il derivato aiuta a calcolare: Alcuni valori in sismografia Caratteristiche campo elettromagnetico Terra Radioattività degli indicatori geofisici nucleari Molti valori in geografia economica Traggono una formula per calcolare la popolazione nel territorio al tempo t.

15 diapositiva

Descrizione della diapositiva:

Problema di geografia Ricavare una formula per calcolare la popolazione in un'area limitata al tempo t.

16 diapositiva

Descrizione della diapositiva:

Soluzione Sia y=y(t) la popolazione. Si consideri la crescita della popolazione per ∆t = t – t0 ∆у = k∙y∙∆t, dove k = kр – kñ è il tasso di crescita della popolazione, (kр è il tasso di natalità, kс è il tasso di mortalità). ∆у/∆t = k∙y come ∆t → 0 otteniamo lim ∆у/∆t = у'. Crescita della popolazione - y' = k∙y. ∆t → 0 Conclusione: il derivato in geografia è combinato con molti dei suoi rami (sismografia, ubicazione e popolazione) oltre che con la geografia economica. Tutto ciò consente di studiare più a fondo lo sviluppo della popolazione e dei paesi del mondo.

17 diapositiva

Descrizione della diapositiva:

Derivato in Economia Il derivato risolve importanti interrogativi: in che direzione cambierà il reddito dello Stato con l'aumento delle tasse o con l'introduzione di dazi doganali? Il reddito dell'impresa aumenterà o diminuirà all'aumentare del prezzo dei suoi prodotti? Per risolvere queste domande è necessario costruire le funzioni di connessione delle variabili di input, che vengono poi studiate con i metodi del calcolo differenziale. Inoltre, utilizzando l'estremo di una funzione nell'economia, si possono trovare la massima produttività del lavoro, il massimo profitto, la massima produzione e i costi minimi.

18 diapositiva

Descrizione della diapositiva:

Problema in economia n. 1 (costi di produzione) Sia y i costi di produzione e x la quantità di produzione, allora x1 è l'aumento della produzione e y1 è l'aumento dei costi di produzione.

19 diapositiva

Descrizione della diapositiva:

20 diapositive

Presentazione sul tema: "L'uso del derivato nella scienza e nella vita" Eseguita da una studentessa del gruppo Phi-17 Dolzhenkova Anastasia Informazioni dalla storia dell'aspetto del derivato: Lo slogan di molti matematici del XVII secolo. era: "Vai avanti e la fiducia nella correttezza dei risultati ti verrà". Il termine "derivato" - ​​(deriva francese - dietro, dietro) fu introdotto nel 1797 da J. Lagrange. Ha anche introdotto la notazione moderna y" , f'. la designazione lim è un'abbreviazione della parola latina limes (confine, confine). Il termine "limite" è stato introdotto da I. Newton. I. Newton ha chiamato la derivata un flusso e la funzione stessa - un fluente. G. Leibniz parlò della relazione differenziale e denotò la derivata come segue: Lagrange Joseph Louis (1736-1813) matematico e meccanico francese Newton:

“Questo mondo era avvolto da una profonda oscurità. Sia la luce! Ed ecco che arriva Newton. A. Pogue.

Isaac Newton (1643-1727) uno dei creatori del calcolo differenziale.

La sua opera principale, I principi matematici della filosofia naturale, ha avuto un enorme impatto sullo sviluppo delle scienze naturali ed è diventata un punto di svolta nella storia delle scienze naturali.

Newton introdusse il concetto di derivata, studiando le leggi della meccanica, rivelandone così il significato meccanico.

Qual è la derivata di una funzione?

La derivata di una funzione in un dato punto è il limite del rapporto tra l'incremento della funzione in quel punto e l'incremento dell'argomento quando l'incremento dell'argomento tende a zero.

Il significato fisico della derivata.

• La velocità è la derivata della distanza rispetto al tempo:
v(t) = S′(t)

• L'accelerazione è la derivata della velocità rispetto al tempo:

a(t) = v′(t) = S′′(t)

Il significato geometrico della derivata: La pendenza della tangente al grafico della funzione è uguale alla derivata di questa funzione, calcolata nel punto di contatto. f′(x) = k = tga Derivato in ingegneria elettrica:

Nelle nostre case, nei trasporti, nelle fabbriche: la corrente elettrica funziona ovunque. Sotto la corrente elettrica comprende il movimento diretto di particelle cariche elettricamente libere.

La caratteristica quantitativa della corrente elettrica è la forza della corrente.

In un circuito elettrico la carica elettrica cambia nel tempo secondo la legge q=q(t). La corrente I è la derivata della carica q rispetto al tempo.

Nell'ingegneria elettrica, il lavoro è principalmente utilizzato corrente alternata.

La corrente elettrica che cambia nel tempo è chiamata corrente alternata. Un circuito in corrente alternata può contenere vari elementi: riscaldatori, bobine, condensatori.

Ottenere una corrente elettrica alternata è basato sulla legge induzione elettromagnetica, la cui formulazione contiene la derivata del flusso magnetico.

Derivato in chimica:

• E in chimica, il calcolo differenziale ha trovato ampia applicazione per la costruzione di modelli matematici di reazioni chimiche e la successiva descrizione delle loro proprietà.
• La chimica è la scienza delle sostanze, le trasformazioni chimiche delle sostanze.
• La chimica studia i modelli di varie reazioni.
• La velocità di una reazione chimica è la variazione della concentrazione di reagenti per unità di tempo.
• Poiché la velocità di reazione v cambia continuamente durante il processo, è solitamente espressa come derivato concentrazioni di reagenti nel tempo.

Derivato in geografia:

L'idea del modello sociologico di Thomas Malthus è che la crescita della popolazione è proporzionale alla popolazione in un dato momento t attraverso N(t), . Il modello malthusiano ha funzionato bene per descrivere la popolazione degli Stati Uniti dal 1790 al 1860. Questo modello non è più valido nella maggior parte dei paesi.

L'integrale e la sua applicazione: Un po' di storia: La storia del concetto di integrale risale ai matematici Grecia antica e Antica Roma. Le opere dello scienziato dell'antica Grecia - Eudosso di Cnido (c. 408-c. 355 aC) sono note per trovare i volumi dei corpi e calcolare le aree delle figure piatte. Il calcolo integrale si diffuse nel XVII secolo. Scienziati: G. Leibniz (1646-1716) e I. Newton (1643-1727) scoprirono indipendentemente l'uno dall'altro e quasi simultaneamente la formula, poi chiamata formula di Newton-Leibniz, che usiamo. Il fatto che un filosofo e un fisico abbiano inventato una formula matematica non sorprende nessuno, perché la matematica è la lingua parlata dalla natura stessa. Il calcolo integrale si diffuse nel XVII secolo. Scienziati: G. Leibniz (1646-1716) e I. Newton (1643-1727) scoprirono indipendentemente l'uno dall'altro e quasi simultaneamente la formula, poi chiamata formula di Newton-Leibniz, che usiamo. Il fatto che un filosofo e un fisico abbiano inventato una formula matematica non sorprende nessuno, perché la matematica è la lingua parlata dalla natura stessa. Simbolo inserito Simbolo inserito Leibniz (1675). Questo segno è una variazione della lettera latina S (la prima lettera della parola somma). La stessa parola integrante inventato J. Bernoulli (1690). Probabilmente deriva dal latino integero, che si traduce come riportare allo stato precedente, restaurare. I limiti dell'integrazione erano già indicati da L. Euler (1707-1783). Nel 1697 apparve il nome di una nuova branca della matematica: il calcolo integrale. È stato introdotto da Bernoulli. In analisi matematica, l'integrale di una funzione è un'estensione del concetto di somma. Il processo per trovare un integrale è chiamato integrazione. Questo processo viene solitamente utilizzato quando si trovano quantità come area, volume, massa, spostamento, ecc., quando viene data la velocità o la distribuzione delle variazioni di questa quantità rispetto a un'altra quantità (posizione, tempo, ecc.). Che cos'è un integrale? L'integrale è uno dei concetti più importanti analisi matematica , che sorge quando si risolvono problemi di reperimento dell'area sotto la curva, la distanza percorsa durante il moto irregolare, la massa di un corpo disomogeneo, ecc., nonché nel problema del ripristino funzioni secondo lei derivato Gli scienziati cercano di esprimere tutti i fenomeni fisici sotto forma di una formula matematica. Una volta che abbiamo una formula, possiamo usarla per calcolare qualsiasi cosa. E l'integrale è uno degli strumenti principali per lavorare con le funzioni. Gli scienziati cercano di esprimere tutti i fenomeni fisici sotto forma di una formula matematica. Una volta che abbiamo una formula, possiamo usarla per calcolare qualsiasi cosa. E l'integrale è uno degli strumenti principali per lavorare con le funzioni. Metodi di integrazione:

• tabulare.
• Riduzione alla trasformazione tabulare dell'integrando in una somma o differenza.
• Integrazione mediante cambio di variabile (sostituzione).
• Integrazione per parti.

Applicazione dell'integrale:

• Matematica
• Calcoli di S cifre.
• La lunghezza dell'arco della curva.
• V corpi in S sezioni parallele.
• V corpi di rivoluzione, ecc.

• Fisica
• Lavoro Una forza variabile.
• S - (percorso) di movimento.
• Calcolo della massa.
• Calcolo del momento d'inerzia di una retta, cerchio, cilindro.
• Calcolo delle coordinate del baricentro.
• La quantità di calore, ecc.

Ministero della Pubblica Istruzione della Regione di Saratov

Professionista autonomo dello Stato Istituto d'Istruzione Regione di Saratov "Politecnico Engels"

APPLICAZIONE DEL DERIVATO IN DIVERSI CAMPI DELLA SCIENZA

Eseguita: Sarkulova Nurgulja Sergeevna

studente del gruppo KShI-216/15

(Progettazione, modellazione e

tecnologia di cucito)

Consulente scientifico:

Verbitskaya Elena Vyacheslavovna

insegnante di matematica GAPOU SO

"Politecnico Engels"

2016

introduzione

Il ruolo della matematica in vari campi delle scienze naturali è molto grande. Non c'è da stupirsi che dicono“La matematica è la regina delle scienze, la sua fisica mano destra, la chimica è rimasta.

L'oggetto della ricerca è il derivato.

L'obiettivo principale è mostrare il significato della derivata non solo in matematica, ma anche in altre scienze, la sua importanza nella vita moderna.

Il calcolo differenziale è una descrizione del mondo che ci circonda, fatta in linguaggio matematico. Il derivato ci aiuta a risolvere con successo non solo problemi di matematica, ma anche compiti pratici in vari campi della scienza e della tecnologia.

La derivata di una funzione viene utilizzata ovunque vi sia un flusso irregolare del processo: si tratta di movimento meccanico irregolare, corrente alternata, reazioni chimiche e decadimento radioattivo della materia, ecc.

Domande chiave e tematiche di questo saggio:

1. La storia dell'origine del derivato.

2. Perché studiare le derivate di funzioni?

3. Dove vengono utilizzati i derivati?

4. Applicazione dei derivati ​​in fisica, chimica, biologia e altre scienze.

5. Conclusioni

Ho deciso di scrivere un articolo sull'argomento "Applicazione del derivato in vari campi della scienza", perché penso che questo argomento sia molto interessante, utile e pertinente.

Nel mio lavoro parlerò dell'applicazione della differenziazione in vari campi della scienza, come chimica, fisica, biologia, geografia, ecc. Dopotutto, tutte le scienze sono indissolubilmente legate, come si vede molto chiaramente nell'esempio dell'argomento Sto considerando.

Applicazione del derivato in vari campi della scienza

Dal corso di algebra del liceo, lo sappiamo già derivato è il limite del rapporto tra l'incremento della funzione e l'incremento del suo argomento poiché l'incremento dell'argomento tende a zero, se tale limite esiste.

L'azione di trovare una derivata è chiamata differenziazione e una funzione che ha una derivata in un punto x è chiamata derivabile in quel punto. Una funzione che è differenziabile in ogni punto di un intervallo è chiamata derivabile su quell'intervallo.

L'onore di scoprire le leggi fondamentali dell'analisi matematica spetta al fisico e matematico inglese Isaac Newton e al matematico, fisico e filosofo tedesco Leibniz.

Newton introdusse il concetto di derivata, studiando le leggi della meccanica, rivelandone così il significato meccanico.

Il significato fisico della derivata: la derivata di una funzioney= f(X) al punto X 0 è la velocità di variazione della funzionef(X) al punto X 0 .

Leibniz è giunto al concetto di derivata risolvendo il problema di tracciare una tangente ad una derivata, spiegandone così il significato geometrico.

Il significato geometrico della derivata è che la funzione derivata in un puntoX 0 uguale alla pendenza della tangente al grafico della funzione tracciata nel punto con l'ascissaX 0 .

Il termine derivato e notazione modernay" , f"Introdotto da J. Lagrange nel 1797.

Il matematico russo del XIX secolo Panfuty Lvovich Chebyshev disse che “quei metodi scientifici che consentono di risolvere un problema comune a tutti attività pratiche una persona, ad esempio, come disporre dei propri mezzi per ottenere il massimo beneficio.

I rappresentanti di varie specialità devono affrontare tali compiti ai nostri giorni:

Gli ingegneri di processo cercano di organizzare la produzione in modo tale da produrre il maggior numero possibile di prodotti;

I designer stanno cercando di sviluppare un dispositivo per navicella spaziale in modo che la massa del dispositivo sia la più piccola;

Gli economisti cercano di pianificare i collegamenti tra l'impianto e le fonti di materie prime in modo tale che i costi di trasporto siano minimi.

Quando studiano un argomento, gli studenti hanno una domanda: "Perché ne abbiamo bisogno?" Se la risposta soddisfa la curiosità, allora possiamo parlare dell'interesse degli studenti. La risposta per l'argomento "Derivata" può essere ottenuta sapendo dove vengono utilizzate le derivate di funzioni.

Per rispondere a questa domanda, possiamo elencare alcune discipline e le loro sezioni in cui vengono utilizzate le derivate.

Derivata in algebra:

1. Tangente al grafico della funzione

Tangente al grafico della funzionef, differenziabile in x di , è una retta passante per il punto (x di ; f(x o )) e avendo una pendenzaf′(x o ).

y= f(x o ) + f′(x o ) (x - x o )

2. Cerca intervalli di funzioni crescenti e decrescenti

Funzioney=f(x) aumenta nell'intervalloX , se per qualcuno ela disuguaglianza. In altre parole - maggior valore argomento corrisponde al valore maggiore della funzione.

Funzioney=f(x) diminuisce nell'intervalloX , se per qualcuno ela disuguaglianza. In altre parole, un valore maggiore dell'argomento corrisponde a un valore minore della funzione.

3. Trovare i punti estremi di una funzione

punto chiamatopunto massimo funzioniy=f(x) se per tuttiX . Viene chiamato il valore della funzione nel punto massimofunzione massima e denotare.

punto chiamatopunto minimo funzioniy=f(x) se per tuttiX dal suo vicinato la disuguaglianza. Viene chiamato il valore della funzione nel punto minimominimo di funzione e denotare.

Sotto l'intorno di un punto capire l'intervallo, dove è un numero positivo abbastanza piccolo.

Vengono chiamati i punti minimo e massimopunti estremi , e vengono chiamati i valori della funzione corrispondenti ai punti estremifunzione estrema .

4. Ricerca di intervalli di convessità e concavità di una funzione

Grafico delle funzioni, è su questo intervalloconvesso , non si trova più in alto di nessuna delle sue tangenti (Fig. 1).

Grafico delle funzioni, differenziabile sull'intervallo, è su questo intervalloconcavo , se il grafico di questa funzione è all'interno dell'intervallo non si trova al di sotto di nessuna delle sue tangenti (Fig. 2).

Il punto di flesso del grafico della funzione è chiamato il punto che separa gli intervalli di convessità e concavità.

5. Trovare i punti di flesso di una funzione

Derivato in fisica:

1. La velocità come derivata del percorso

2. Accelerazione come derivata della velocitàun =

3. Tasso di decadimento degli elementi radioattivi 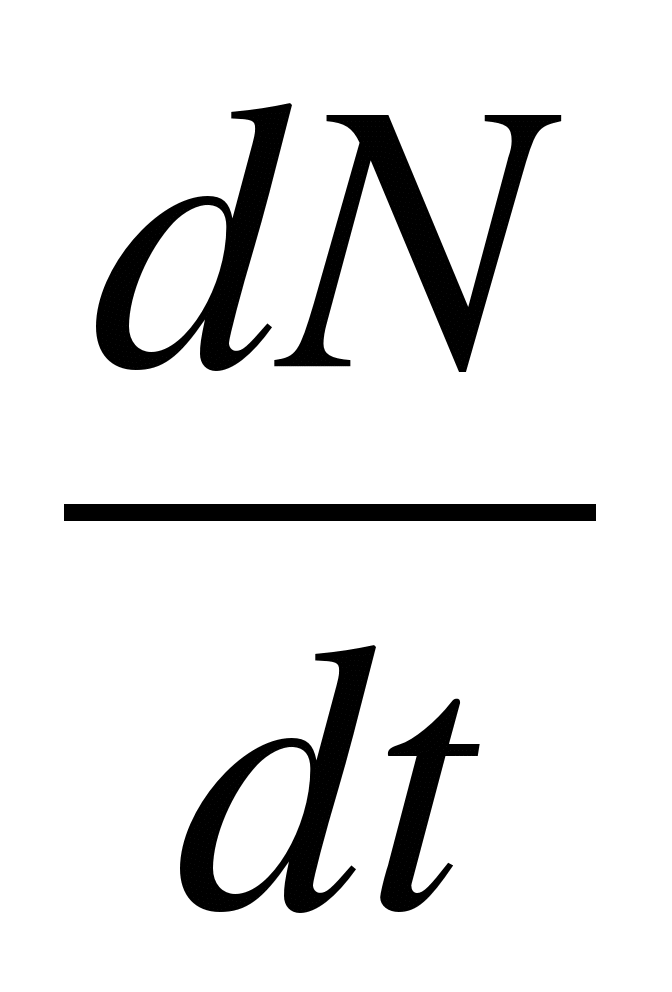= - λN

E anche in fisica, la derivata viene utilizzata per calcolare:

Velocità del punto materiale

La velocità istantanea come significato fisico della derivata

Corrente AC istantanea

Valore istantaneo dell'EMF dell'induzione elettromagnetica

Massima potenza

Derivato in chimica:

E in chimica, il calcolo differenziale ha trovato ampia applicazione per la costruzione di modelli matematici di reazioni chimiche e la successiva descrizione delle loro proprietà.

Un derivato in chimica viene utilizzato per determinare una cosa molto importante: la velocità di una reazione chimica, uno dei fattori decisivi che devono essere presi in considerazione in molti settori dell'attività scientifica e industriale.. V(t) = p'(t)

Quantità

in-va alla volta t 0

p = p(t 0 )

Funzione

Intervallo di tempo

∆t = t–t 0

Incremento argomento

Cambio di quantità

∆p=p(t 0 + ∆t) – p(t 0 )

Incremento della funzione

Velocità media di una reazione chimica

∆p/∆t

Rapporto tra incremento della funzione e incremento dell'argomento

Derivato in biologia:

Una popolazione è un insieme di individui di una determinata specie che occupano una determinata area del territorio all'interno dell'area di distribuzione della specie, incrociandosi liberamente tra loro e parzialmente o completamente isolati dalle altre popolazioni, ed è anche un'unità elementare di evoluzione.

P \u003d x' (t)

Derivato in geografia:

1. Alcuni significati in sismografia

2. Caratteristiche del campo elettromagnetico della terra

3. Radioattività dei parametri geofisici nucleari

4. Molti significati in geografia economica

5. Ricavare una formula per calcolare la popolazione nel territorio al tempo t.

y'= a y

L'idea del modello sociologico di Thomas Malthus è che la crescita della popolazione è proporzionale alla popolazione in un dato momento da t a N(t).Il modello di Malthus ha funzionato bene per descrivere la popolazione degli Stati Uniti dal 1790 al 1860. Questo modello non è più valido nella maggior parte dei paesi.

Derivato in ingegneria elettrica:

Nelle nostre case, nei trasporti, nelle fabbriche: la corrente elettrica funziona ovunque. Sotto la corrente elettrica comprende il movimento diretto di particelle cariche elettricamente libere.

La caratteristica quantitativa della corrente elettrica è la forza della corrente.

In un circuito elettrico la carica elettrica cambia nel tempo secondo la legge q=q(t). La corrente I è la derivata della carica q rispetto al tempo.

Nell'ingegneria elettrica, viene utilizzato principalmente il funzionamento in CA.

La corrente elettrica che cambia nel tempo è chiamata corrente alternata. Un circuito in corrente alternata può contenere vari elementi: riscaldatori, bobine, condensatori.

La produzione di corrente elettrica alternata si basa sulla legge dell'induzione elettromagnetica, la cui formulazione contiene la derivata del flusso magnetico.

Derivato in economia:

L'economia è la base della vita e il calcolo differenziale, un apparato per l'analisi economica, occupa un posto importante in essa. Il compito fondamentale dell'analisi economica è studiare le relazioni delle grandezze economiche sotto forma di funzioni.

La derivata in economia risolve importanti domande:

1. In che direzione cambierà il reddito dello Stato con l'aumento delle tasse o con l'introduzione di dazi doganali?

2. Il fatturato dell'azienda aumenterà o diminuirà con l'aumento del prezzo dei suoi prodotti?

Per risolvere queste domande è necessario costruire le funzioni di connessione delle variabili di input, che vengono poi studiate con i metodi del calcolo differenziale.

Inoltre, utilizzando l'estremo della funzione (derivata) nell'economia, puoi trovare la massima produttività del lavoro, il massimo profitto, la massima produzione e i costi minimi.

CONCLUSIONE: il derivato viene utilizzato con successo per risolvere vari problemi applicati nella scienza, nella tecnologia e nella vita

Come si può vedere da quanto sopra, l'uso della derivata di una funzione è molto vario, e non solo nello studio della matematica, ma anche in altre discipline. Pertanto, possiamo concludere che lo studio dell'argomento: "La derivata di una funzione" avrà la sua applicazione in altri argomenti e materie.

Eravamo convinti dell'importanza di approfondire l'argomento "Derivato", il suo ruolo nello studio dei processi della scienza e della tecnologia, la possibilità di progettare secondo eventi reali modelli matematici e risolvere problemi importanti.

“La musica può elevare o lenire l'anima,
La pittura è piacevole alla vista,
Poesia - per risvegliare i sentimenti,
Filosofia - per soddisfare i bisogni della mente,
L'ingegneria è migliorare il lato materiale della vita delle persone,
MAla matematica può raggiungere tutti questi obiettivi”.

Così disse il matematico americanoMaurizio Kline.

Bibliografia:

1. Bogomolov N.V., Samoylenko I.I. Matematica. - M.: Yurayt, 2015.

2. V. P. Grigoriev e Yu. A. Dubinsky, Elementi di matematica superiore. - M.: Accademia, 2014.

3. Bavrin II Fondamenti di matematica superiore. - M.: scuola di Specializzazione, 2013.

4. Bogomolov N.V. Officine matematica. - M.: Scuola superiore, 2013.

5. Bogomolov N.V. Raccolta di problemi in matematica. - M.: Otarda, 2013.

6. Rybnikov KA Storia della matematica, Moscow University Press, M, 1960.

7. Vinogradov Yu.N., Gomola AI, Potapov VI, Sokolova E.V. - M.:Centro editoriale "Accademia", 2010

8 . Bashmakov MI Matematica: algebra e inizi dell'analisi matematica, geometria. - M.: Centro Editoriale "Accademia", 2016

Fonti periodiche:

Giornali e riviste: "Matematica", " Lezione pubblica»

Utilizzo di risorse Internet, biblioteche elettroniche:

www:egetutor.ru

matematika-na5.norod.ru

Indietro avanti

Attenzione! L'anteprima della diapositiva è solo a scopo informativo e potrebbe non rappresentare l'intera portata della presentazione. Se sei interessato a questo lavoro, scarica la versione completa.

Tipo di lezione: integrato.

Lo scopo della lezione: studiare alcuni aspetti dell'applicazione della derivata in vari campi della fisica, della chimica, della biologia.

Compiti: ampliare gli orizzonti e l'attività cognitiva degli studenti, lo sviluppo pensiero logico e la capacità di applicare le proprie conoscenze.

Supporto tecnico: lavagna interattiva; computer e disco.

DURANTE LE LEZIONI

I. Momento organizzativo

II. Stabilire l'obiettivo della lezione

- Vorrei tenere una lezione sotto il motto di Alexei Nikolaevich Krylov, matematico e costruttore navale sovietico: "La teoria senza pratica è morta o inutile, la pratica senza teoria è impossibile o perniciosa".

Esaminiamo i concetti di base e rispondiamo alle domande:

Qual è la definizione di base di una derivata?
– Cosa sai della derivata (proprietà, teoremi)?
– Conosci qualche esempio di problemi derivati ​​in fisica, matematica e biologia?

Considerazione della definizione di base della derivata e della sua giustificazione (risposta alla prima domanda):

Derivato è uno dei concetti fondamentali della matematica. La capacità di risolvere problemi utilizzando la derivata richiede una buona conoscenza materiale teorico capacità di condurre ricerche in diverse situazioni.

Pertanto, oggi nella lezione consolideremo e sistematizzeremo le conoscenze acquisite, considereremo e valuteremo il lavoro di ciascun gruppo e, utilizzando l'esempio di alcuni compiti, mostreremo come utilizzare la derivata per risolvere altri problemi e compiti non standard utilizzando la derivata.

III. Spiegazione del nuovo materiale

1. La potenza istantanea è la derivata del lavoro rispetto al tempo:

W = lim ∆A/∆t ∆A – cambio di lavoro.

2. Se il corpo ruota attorno ad un asse, l'angolo di rotazione è una funzione del tempo t
Allora la velocità angolare è:

W = lim Δφ/Δt = φ׳(t) Δ t → 0

3. La forza attuale è un derivato Ι = lim Δg/Δt = g′, dove g- carica elettrica positiva trasferita nel tempo attraverso la sezione del conduttore Δt.

4. Lascia ∆Qè la quantità di calore necessaria per modificare la temperatura Δt tempo, allora lim ΔQ/Δt = Q′ = C – calore specifico.

5. Il problema della velocità di una reazione chimica

m(t) – m(t0) – la quantità di una sostanza che reagisce nel tempo t0 prima t

V= lim ∆m/∆t = m ∆t → 0

6. Sia m la massa della sostanza radioattiva. Tasso di decadimento radioattivo: V = lim ∆m/∆t = m׳(t) ∆t→0

In forma differenziata, la legge del decadimento radioattivo ha la forma: dN/dt = – λN, dove Nè il numero di nuclei che non sono decaduti nel tempo t.

Integrando questa espressione, otteniamo: dN/N = – λdt ∫dN/N = – λ∫dt lnN = – λt + c, c = cost a t = 0 numero di nuclei radioattivi N = N0, quindi abbiamo: log N0 = cost, Di conseguenza

n N = – λt + ln N0.

Potenziando questa espressione otteniamo:

è la legge del decadimento radioattivo, dove N0è il numero di core alla volta t0 = 0, Nè il numero di nuclei che non sono decaduti nel tempo t.

7. Secondo l'equazione di scambio termico di Newton, la portata termica dQ/dtè direttamente proporzionale alla superficie della finestra S e alla differenza di temperatura ΔT tra il vetro interno ed esterno e inversamente proporzionale al suo spessore d:

dQ/dt =A S/d ∆T

8. Il fenomeno della diffusione è il processo per stabilire una distribuzione di equilibrio

All'interno delle fasi di concentrazione. La diffusione va di lato, equalizzando le concentrazioni.

m = D ∆c/∆x c – concentrazione
m = D c׳x x - coordinata, D- coefficiente di diffusione

Legge di Fick:

9. Si sapeva che anche il campo elettrico eccita cariche elettriche, o un campo magnetico che ha un'unica sorgente: una corrente elettrica. James Clark Maxwell ha introdotto un emendamento alle leggi dell'elettromagnetismo scoperto prima di lui: quando si verifica anche un campo magnetico campo elettrico. Piccolo a prima vista, l'emendamento ha avuto conseguenze grandiose: è apparso un oggetto fisico completamente nuovo, anche se sulla punta della penna, Onda elettromagnetica. Maxwell possedeva magistralmente, in contrasto con Faraday, che sembrava possibile la sua esistenza, dedusse l'equazione per il campo elettrico:

∂E/∂x = M∂B/Mo ∂t Mo = cost t

Una variazione del campo elettrico provoca la comparsa di un campo magnetico in qualsiasi punto dello spazio, in altre parole, la velocità di variazione del campo elettrico determina l'entità del campo magnetico. Sotto una grande corrente elettrica - un grande campo magnetico.

IV. Consolidamento degli studiati

– Abbiamo studiato la derivata e le sue proprietà. Vorrei leggere l'affermazione filosofica di Gilbert: “Ogni persona ha una certa prospettiva. Quando questo orizzonte si restringe all'infinitamente piccolo, si trasforma in un punto. Poi la persona dice che questo è il suo punto di vista.
Proviamo a misurare il punto di vista sull'applicazione della derivata!

Trama "Foglia"(applicazione della derivata in biologia, fisica, vita)

Considera la caduta come un movimento non uniforme a seconda del tempo.

Così: S = S(t) V = S′(t) = x′(t), a = V′(t) = S″(t)

(Rilievo teorico: il significato meccanico della derivata).

1. Risoluzione dei problemi

Risolvi i problemi da solo.

2. F = ma F = mV′ F = mS″

Scriviamo la II legge di Porton e, tenendo conto del significato meccanico della derivata, la riscriviamo nella forma: F = mV′ F = mS″

La trama di "Lupi, Gopher"

Torniamo alle equazioni: Consideriamo le equazioni differenziali di crescita e decrescita esponenziale: F = ma F = mV" F = mS""
La soluzione di molti problemi di fisica, biologia tecnica e scienze sociali si riduce al problema della ricerca di funzioni f"(x) = kf(x), soddisfando l'equazione differenziale, dove k = cost .

Formula umana

Un uomo è tante volte più grande di un atomo quanto è più piccolo di una stella:

Quindi ne consegue che
Questa è la formula che determina il posto dell'uomo nell'universo. In accordo con esso, le dimensioni di una persona rappresentano la media proporzionale della stella e dell'atomo.

Vorrei concludere la lezione con le parole di Lobachevsky: "Non esiste una singola area della matematica, non importa quanto astratta possa essere, che un giorno non sarà applicabile ai fenomeni del mondo reale".

V. Soluzione dei numeri della collezione:

Risoluzione dei problemi indipendente a bordo, analisi collettiva delle soluzioni dei problemi:

№ 1 Trova la velocità del punto materiale alla fine del 3° secondo, se il movimento del punto è dato dall'equazione s = t^2 –11t + 30.

№ 2 Il punto si muove rettilineo secondo la legge s = 6t – t^2. A che punto la sua velocità sarà zero?

№ 3 Due corpi si muovono in linea retta: uno secondo la legge s \u003d t^3 - t^2 - 27t, l'altro - secondo la legge s \u003d t^2 + 1. Determina il momento in cui le velocità di questi i corpi sono uguali.

№ 4 Per un'auto che si muove a una velocità di 30 m/s, lo spazio di arresto è determinato dalla formula s(t) =30t-16t^2, dove s(t) è la distanza in metri, t è il tempo di frenata in secondi . Quanto tempo ci vuole per decelerare prima che l'auto si fermi completamente? Qual è la distanza percorsa dall'auto dall'inizio della frenata fino all'arresto completo?

№5 Un corpo di massa 8 kg si muove in linea retta secondo la legge s = 2t^2+ 3t - 1. Trova l'energia cinetica del corpo (mv^2/2) 3 secondi dopo l'inizio del movimento.

Soluzione: Trova la velocità del corpo in qualsiasi momento:
V=ds/dt=4t+3
Calcola la velocità del corpo al tempo t = 3:
V t \u003d 3 \u003d 4 * 3 + 3 \u003d 15 (m / s).
Determiniamo l'energia cinetica del corpo al tempo t = 3:
mv2/2 = 8 - 15^2 /2 = 900 (J).

№6 Trova l'energia cinetica del corpo 4 s dopo l'inizio del movimento, se la sua massa è 25 kg e la legge del moto è s = 3t^2-1.

№7 Un corpo la cui massa è di 30 kg si muove in linea retta secondo la legge s = 4t^2 + t. Dimostra che il movimento del corpo avviene sotto l'azione di una forza costante.
Soluzione: Abbiamo s" = 8t + 1, s" = 8. Pertanto, a(t) = 8 (m/s^2), cioè, con una data legge del moto, il corpo si muove con un'accelerazione costante di 8 m /s^2. Inoltre, poiché la massa del corpo è costante (30 kg), allora, secondo la seconda legge di Newton, anche la forza che agisce su di esso F = ma = 30 * 8 = 240 (H) è un valore costante.

№8 Un corpo di massa 3 kg si muove in linea retta secondo la legge s(t) = t^3 - 3t^2 + 2. Trova la forza che agisce sul corpo al tempo t = 4s.

№9 Il punto materiale si muove secondo la legge s = 2t^3 – 6t^2 + 4t. Trova la sua accelerazione alla fine del 3° secondo.

VI. Applicazione della derivata in matematica:

La derivata in matematica mostra l'espressione numerica del grado di variazione di una quantità situata nello stesso punto sotto l'influenza di varie condizioni.

La formula derivata risale al XV secolo. Il grande matematico italiano Tartaglia, considerando e sviluppando la questione - quanto dipende la gittata del proiettile dall'inclinazione del fucile - la usa nei suoi scritti.

La formula derivata si trova spesso nelle opere di famosi matematici del XVII secolo. È usato da Newton e Leibniz.

Il noto scienziato Galileo Galilei dedica un intero trattato al ruolo della derivata in matematica. Poi il derivato e le varie presentazioni con la sua applicazione cominciarono a trovarsi nelle opere di Descartes, del matematico francese Roberval e dell'inglese Gregory. Un grande contributo allo studio del derivato è stato dato da menti come Lopital, Bernoulli, Langrange e altri.

1. Traccia ed esplora la funzione:

Soluzione a questo problema:

Un momento di relax

VII. Applicazione della derivata in fisica:

Quando si studiano determinati processi e fenomeni, sorge spesso il problema di determinare la velocità di questi processi. La sua soluzione porta al concetto di derivata, che è il concetto base del calcolo differenziale.

Il metodo del calcolo differenziale è stato creato nel XVII e XVIII secolo. I nomi di due grandi matematici, I. Newton e G.V. Leibniz.

Newton arrivò alla scoperta del calcolo differenziale quando risolveva problemi sulla velocità di un punto materiale in un dato momento (velocità istantanea).

In fisica, la derivata viene utilizzata principalmente per calcolare il più grande o i valori più piccoli qualsiasi quantità.

Risoluzione dei problemi:

№1 Energia potenziale u il campo di una particella in cui ce n'è un'altra, esattamente la stessa particella ha la forma: U = a/r 2 – b/r, dove un e b sono costanti positive, r- distanza tra le particelle. Trova: a) valore r0 corrispondente alla posizione di equilibrio della particella; b) verificare se tale situazione è stabile; in) Fmax il valore della forza di attrazione; d) rappresentare grafici di dipendenza approssimativi U(r) e Fr).

Soluzione di questo problema: determinare r0 corrispondente alla posizione di equilibrio della particella, indaghiamo f = U(r) all'estremo.

Utilizzando la relazione tra l'energia potenziale del campo

u e F, poi F = -dU/dr, noi abbiamo F = – dU/dr = – (2a/r3+ b/r2) = 0; in cui r = r0; 2a/r3 = b/r2 => r0 = 2a/b; L'equilibrio stabile o instabile è determinato dal segno della derivata seconda:
d2U/dr02= dF/dr0 = – 6a/r02 + 2b/r03 = – 6a/(2a/b)4 + 2b/(2a/b)3 = (– b4/8a3)< 0 ;
l'equilibrio è stabile.

Per determinare Fmax attrazione, indago la funzione per gli estremi: F = 2a/r3 - b/r2;
dF/dr = –6a/r4 + 2b/r3 = 0; a r = r1 = 3a/b; sostituendo, ottengo Fmax = 2a/r31 - b/r31 = – b3/27a2; U(r) = 0; a r = a/b; U(r)min a r = 2, a/b = r0;F = 0; F(r)max a r = r1 = 3a/b;
Risposta: F(r)max a r = r1 = 3a/b;

№2 Circuito con resistenza esterna R = 0,9 ohm alimentato da una batteria k = 36 fonti identiche, ognuna delle quali ha una fem E=2 A e resistenza interna r0 = 0,4 ohm. La batteria include n gruppi collegati in parallelo e ciascuno di essi contiene m batterie collegate in serie. A quali valori m, n riceverà il massimo J nell'esterno R.

Soluzione a questo problema:

Quando le batterie sono collegate in serie E gr = m* e ; rgr = r0*m;
e con collegamento in parallelo degli stessi rbat = r0m/n; e baht = m* E,
Legge di Ohm J=m e /(R+ r0m/n) = m e n/(nR + r0m)
Perché Kè il numero totale di batterie, quindi k = mn;
J=k e /(nR + r0m) = k e /(nR + kr0/n);
Per trovare la condizione in cui J corrente nel circuito massimo esplorare la funzione J = J(n) extremum prendendo la derivata rispetto a n e uguagliandola a zero.
J'n - (k e (R - kr0/n2))/ (nR + kr0/n)2 = 0;
n2 = kr/R
n = √kr/R = √3,6*0,4/0,9 = 4;
m = k/n = 36/4 = 9;
in cui Jmax = k e / (nR + mr0) \u003d 36 * 2 / (4 * 0,9 + 9 * 0,4) \u003d 10 A;

Risposta: n=4, m=9.

№3 Piattaforma di massa M inizia a muoversi a destra sotto l'azione di una forza costante F. La sabbia viene versata su di esso da un bunker fermo. La velocità di caricamento è costante e uguale a µ kg/s. Trascurando l'attrito, trovare la dipendenza dal tempo di accelerazione a della piattaforma durante il carico. Determina l'accelerazione a1 piattaforma nel caso in cui la sabbia non venga versata sulla piattaforma, ma da quella riempita fuoriesca dal foro presente sul fondo a velocità costante µ kg/s.

Soluzione a questo problema: considera prima il caso in cui la sabbia viene versata sulla piattaforma
Il moto del sistema piattaforma-sabbia può essere descritto usando la seconda legge di Newton:
dP/dt = FΣ
Pè lo slancio del sistema piattaforma-sabbia, FΣè la forza che agisce sul sistema piattaforma-sabbia.
Se attraverso p indichiamo lo slancio della piattaforma, quindi possiamo scrivere: dp/dt = F
Troviamo la variazione della quantità di moto della piattaforma su un intervallo di tempo infinitesimo Δ t: Δ p = (M + µ(t + Δ t))(u +Δ u) – (M + µt)u = FΔ t;
dove tu– velocità della piattaforma.
Aprendo le parentesi ed effettuando le riduzioni otteniamo:
Dp = µuΔ t+MΔ u+ Δ µut +Δ uuΔ t = FΔ t
Dividere per Δt e passare al limite Δ t→ 0
Mdu/dt + µtdu/dt + µu= FA o d[(M + µt)u]/dt = F
Questa equazione può essere integrata assumendo che la velocità iniziale della piattaforma sia zero: (M + µt)u = Ft.
Di conseguenza: u = Ft/(M + µt)
Quindi, accelerazione della piattaforma: a = du/dt = (F(M + µt) – Ftµ)/(M + µt) 2 = FM / (M + µt) 2

Considera il caso in cui la sabbia fuoriesce da una piattaforma piena.
Variazione della quantità di moto in un breve periodo di tempo:
Δ p = (M – µ(t +Δ t))(u+Δ u) +Δ µtu – (M – µt)u = FΔ t
Termine Δ µtuè la quantità di moto della quantità di sabbia che fuoriesce dalla piattaforma durante il tempo Δ t. Quindi:
Δ p = MΔ u-µtΔ tu-Δ µtΔ u=FΔ t
Dividi per Δ t e passare al limite Δ t→ 0
(M – µt)du/dt = F
O a1= du/dt= F/(M – µt)

Risposta: a = FM / (M + µt) 2 , a1= F/(M – µt)

VIII.Lavoro indipendente:

Trova le derivate di funzioni:

La linea y \u003d 2x è tangente alla funzione: y \u003d x 3 + 5x 2 + 9x + 3. Trova l'ascissa del punto di contatto.

IX. Riassumendo la lezione:

- Quali erano gli argomenti della lezione?
- Cosa hai imparato a lezione?
Quali fatti teorici sono stati riassunti nella lezione?
– Quali sono stati i compiti più difficili considerati? Come mai?

Bibliografia:

1. Amelkin V.V., Sadovsky A.P. Modelli matematici ed equazioni differenziali. - Minsk: Scuola superiore, 1982. - 272 p.
2. Amelkin V.V. Equazioni differenziali nelle applicazioni. M.: Scienza. Edizione principale della letteratura fisica e matematica, 1987. - 160p.
3. Erugin NP Libro per la lettura sul corso generale delle equazioni differenziali. - Minsk: Scienza e tecnologia, 1979. - 744 p.
4. .Rivista "Potenziale" Novembre 2007 №11
5. "Algebra e gli inizi dell'analisi" Grado 11 S.M. Nikolsky, M.K. Potapov e altri.
6. "Algebra e analisi matematica" N.Ya. Vilenkin e altri.
7. "Matematica" V.T. Lisichkin, IL Soloveichik, 1991

Un compito. La funzione di costo ha la forma e il reddito di produzione X unità di beni è definita come segue:

Determinare il valore di uscita ottimale per il produttore x0.

Soluzione:

Profitto P(x) =D(X) - C(x), dove D(X) - reddito da produzione X unità di prodotto.

La funzione profitto è simile a:

Trova la derivata della funzione profitto:

Ovviamente, P "(x)> 0 a X< 100 così valore più alto ci sono profitti sul segmento R(100) = 399 900. Ora troviamo il massimo valore di profitto nell'intervallo (100; + ∞). C'è un punto critico x= 200. Allo stesso tempo P "(x)> 0 a 100< X < 200 и R" (X)< 0 a X> 200, cioè x= 200 - valore massimo P(x) sull'intervallo (100; + ∞).

R(200) = 419 900 > R(100), così X all'ingrosso = 200 (unità).

Un compito. La cementeria produce X tonnellate di cemento al giorno. Secondo il contratto, deve fornire all'impresa edile almeno 20 tonnellate di cemento al giorno. La capacità produttiva dell'impianto è tale che la produzione di cemento non può superare le 90 tonnellate al giorno.

Determina a quale volume di produzione i costi unitari saranno i maggiori (minimi), se la funzione di costo ha la forma:

K=-x3+98x2+200x. I costi unitari saranno K/x=-x2+98x+200

Soluzione:

Il problema si riduce a trovare i valori più grandi e più piccoli della funzione

y= - x2+98x+200. Nel mezzo.

DIV_ADBLOCK1021">

6 Applicazione del derivato in medicina

L'applicazione del calcolo differenziale in medicina si riduce al calcolo della velocità. Ad esempio, le velocità delle reazioni di recupero e le velocità del processo di rilassamento.

La reazione del corpo al farmaco somministrato può essere espressa in un aumento della pressione sanguigna, un cambiamento della temperatura corporea, un cambiamento del polso o altri indicatori fisiologici. Il grado di reazione dipende dal farmaco prescritto, dalla sua dose. Usando il derivato, puoi calcolare a quale dose del farmaco è massima la reazione del corpo. Usando la seconda derivata, è possibile determinare le condizioni in cui la velocità di processo è più sensibile a qualsiasi influenza

Un compito Facciamo finta che X indica la dose del farmaco prescritto, aè una funzione del grado di reazione. y=f(x)=x²(a-x), dove unè una costante positiva. A che valore X risposta massima?

Soluzione:

https://pandia.ru/text/80/244/images/image137_6.gif" width="116" height="24">. Quindi con ..gif" width="49" height="42"> - il livello di dose che dà la risposta massima.

I punti di flesso sono importanti in biochimica, poiché definiscono le condizioni in cui una certa quantità, come la velocità di un processo, è più (o meno) sensibile a qualsiasi influenza.

Un compito. Come risultato di una significativa perdita di sangue, il contenuto di ferro nel sangue è diminuito di 210 mg. Carenza di ferro a causa del suo recupero nel tempo t diminuisce secondo la legge mg (t - giorno). Trova la dipendenza del tasso di recupero del ferro nel sangue in tempo. Calcola questa velocità al momento t=0 e dopo 7 giorni.

Soluzione:

Tasso di recupero del ferro:

https://pandia.ru/text/80/244/images/image144_5.gif" width="33" height="18"> il tasso di recupero è di 30 mg/giorno. Dopo 7 giorni, il tasso di recupero è di 11,1 mg /giorno giorni:

Il processo di rilassamento è il processo di riportare il sistema allo stato di equilibrio stabile da cui è stato prelevato. In molti casi (soprattutto con una singola esposizione), questo processo è descritto dall'equazione esponenziale. Il suo significato fisico è: - questo è il tempo durante il quale la deviazione iniziale dell'attività di ricerca" href="/text/category/nauchno_issledovatelmzskaya_deyatelmznostmz/" rel ="bookmark">attività di ricerca e produzione. Ad esempio, ingegneri di processo nel determinare l'efficacia della produzione chimica, chimici che sviluppano farmaci per la medicina e l'agricoltura, nonché medici e agronomi che usano questi farmaci per curare le persone e applicarli al suolo. Alcune reazioni sono quasi istantanee, mentre altre sono molto lente. A vita reale per risolvere i problemi di produzione nell'industria medica, agricola e chimica, è importante conoscere le velocità di reazione delle sostanze chimiche.

Lascia che la funzione m=m(t), dove m- la quantità di una sostanza che è entrata in una reazione chimica alla volta t. Incremento di tempo Δt corrisponderà all'incremento ∆m le quantità m. Atteggiamento ∆m/∆tè la velocità media di una reazione chimica in un periodo di tempo Δt. Il limite di questo rapporto quando si sforza Δt a zero è la velocità di una reazione chimica in un dato momento.

Un compito. La relazione tra la massa x di una sostanza ottenuta come risultato di una reazione chimica e del tempo t espresso dall'equazione https://pandia.ru/text/80/244/images/image151_5.gif" width="283" height="30 src=">

Un compito. La concentrazione della soluzione varia nel tempo secondo la legge: . Trova il tasso di dissoluzione.

Soluzione:

Il tasso di scioglimento è calcolato utilizzando la derivata:

https://pandia.ru/text/80/244/images/image154_4.gif" width="139" height="42 src=">. Ottieni la formula per il tasso di crescita della popolazione.

Soluzione:

Un compito. Dipendenza dalla produzione giornaliera di latte y in litri dall'età delle vacche X in anni è determinato dall'equazione , dove x>2. Trova l'età delle vacche da latte in cui la produzione giornaliera di latte sarà la più alta.

Soluzione:

https://pandia.ru/text/80/244/images/image161_4.gif" width="77" height="23 src=">

(anni) - il punto massimo, l'età delle vacche da latte, in cui la produzione giornaliera di latte sarà la maggiore.

Conclusione

In questo lavoro viene considerato uno dei concetti più importanti dell'analisi matematica: la derivata di una funzione dal punto di vista della sua applicazione pratica. Con l'aiuto del derivato, puoi risolvere un'ampia varietà di problemi relativi a qualsiasi area. attività umana. In particolare, con l'aiuto delle derivate, è possibile studiare in dettaglio le funzioni, costruire i loro grafici in modo più accurato, risolvere equazioni e disequazioni, dimostrare identità e disequazioni e trovare i valori più grandi e più piccoli delle quantità.

Per tutti i suddetti ambiti di applicazione della derivata sono stati selezionati e sintetizzati in una raccolta circa duecento problemi. Ogni sezione della raccolta inizia con un breve riassunto dei fondamenti teorici, contiene compiti tipici con soluzioni e serie di esercizi per soluzione indipendente. Questi compiti ampliano i propri orizzonti e aumentano l'interesse per il derivato. Possono essere interessanti e utili per gli studenti appassionati di matematica.

Letteratura

1. Compiti di Bogomolov in matematica: libro di testo per i college. – M.: Otarda, 2005.

2. Bogomolov: libro di testo. per i college /, - M .: Bustard, 2010.

3. Bogomolov. Compiti didattici: libro di testo. indennità per i college /, - M.: Bustard, 2005.

4. Istomina: domande e risposte: libro di testo. indennità per le università. - Rostov n/d: Phoenix, 2002.

5. Lisichkin: libro di testo. indennità per le scuole tecniche /, - M.: Superiore. scuola, 1991.

6. Analisi matematica di Nikolsky: libro di testo. indennità per gli studenti. suzov.- M.: Otarda, 2012.

7. Omelchenko: libro di testo. indennità per i college. - Rostov n/d: Phoenix, 2007.

8. Filimonova: libro di testo. indennità per i college. – Rostov n/a: Phoenix, 2013.