Matricas rangs īsi. Matricas ranga noteikšana. Matricas ranga aprēķins pēc definīcijas. Matricas ranga aprēķināšana, izmantojot elementāras transformācijas
Apsveriet taisnstūra matricu. Ja šajā matricā mēs izvēlamies patvaļīgi k līnijas un k kolonnas, tad elementi atlasīto rindu un kolonnu krustpunktā veido k-tās kārtas kvadrātmatricu. Šīs matricas determinants tiek saukts k-tās kārtas nepilngadīgais matrica A. Acīmredzot matricai A ir jebkuras kārtas minori no 1 līdz mazākajam no skaitļiem m un n. Starp visiem matricas A nepilngadīgajiem, kas nav nulle, ir vismaz viens nepilngadīgais, kura secība ir vislielākā. Tiek izsaukta lielākā no dotās matricas nepilngadīgo kārtas vērtībām, kas nav nulles rangs matricas. Ja matricas A rangs ir r, tad tas nozīmē, ka matricai A ir mazākā kārta, kas nav nulle r, bet katrs nepilngadīgais pasūtījums lielāks par r, ir vienāds ar nulli. Matricas A rangu apzīmē ar r(A). Ir skaidrs, ka attiecības
Matricas ranga aprēķināšana, izmantojot nepilngadīgos
Matricas rangs tiek noteikts vai nu ar mazo robežu metodi, vai ar metodi elementāras pārvērtības. Aprēķinot matricas rangu pirmajā veidā, no zemākas kārtas nepilngadīgajiem jāpāriet uz augstākas pakāpes nepilngadīgajiem. Ja jau ir atrasts matricas A k-tās kārtas nepilngadīgais D, kas nav nulle, tad jāaprēķina tikai (k + 1) kārtas nepilngadīgie, kas robežojas ar mazo D, t.i. satur to kā nepilngadīgo. Ja tie visi ir nulle, tad matricas rangs ir k.
1. piemērsAtrodiet matricas rangu pēc nepilngadīgo robežu metodes
.
Risinājums.Sākam ar 1. kārtas nepilngadīgajiem, t.i. no matricas A elementiem. Izvēlēsimies, piemēram, mazo (elementu) М 1 = 1, kas atrodas pirmajā rindā un pirmajā kolonnā. Robežojoties ar otrās rindas un trešās kolonnas palīdzību, iegūstam minoru M 2 = , kas atšķiras no nulles. Tagad mēs pievēršamies 3. kārtas nepilngadīgajiem, kas robežojas ar M 2 . Ir tikai divi no tiem (varat pievienot otro vai ceturto kolonnu). Mēs tos aprēķinām: 
=
0. Tādējādi visi trešās kārtas pierobežas nepilngadīgie izrādījās vienādi ar nulli. Matricas A rangs ir divi.
Matricas ranga aprēķināšana, izmantojot elementāras transformācijas
ElementāriTiek sauktas šādas matricas transformācijas:
1) jebkuru divu rindu (vai kolonnu) permutācija,
2) rindu (vai kolonnu) reizinot ar skaitli, kas nav nulle,
3) vienai rindai (vai kolonnai) pievienojot citu rindu (vai kolonnu), kas reizināta ar kādu skaitli.
Abas matricas sauc ekvivalents, ja vienu no tiem iegūst no otra ar ierobežotas elementāru pārveidojumu kopas palīdzību.
Ekvivalentās matricas, vispārīgi runājot, nav vienādas, bet to kārtas ir vienādas. Ja matricas A un B ir līdzvērtīgas, tad to raksta šādi: A~b.
KanonisksMatrica ir matrica, kuras galvenās diagonāles sākumā pēc kārtas ir vairāki 1 (kuru skaits var būt nulle), un visi pārējie elementi ir vienādi ar nulli, piemēram,
.
Ar elementāru rindu un kolonnu transformāciju palīdzību jebkuru matricu var reducēt uz kanonisku. Kanoniskās matricas rangs ir vienāds ar matricu skaitu tās galvenajā diagonālē.
2. piemērsAtrodiet matricas rangu
un izveidojiet to kanoniskā formā.
Risinājums. Atņemiet pirmo rindu no otrās rindas un pārkārtojiet šīs rindas:
.
Tagad no otrās un trešās rindas atņemiet pirmo, attiecīgi reizinātu ar 2 un 5:
;
atņemiet pirmo no trešās rindas; mēs iegūstam matricu
kas ir ekvivalents matricai A, jo to iegūst no tās, izmantojot ierobežotu elementāru pārveidojumu kopu. Acīmredzot matricas B rangs ir 2, un līdz ar to r(A)=2. Matricu B var viegli reducēt uz kanonisko. Atņemot pirmo kolonnu, kas reizināta ar piemērotiem skaitļiem, no visiem nākamajiem, mēs visus pirmās rindas elementus, izņemot pirmo, pārvēršam uz nulli, un atlikušo rindu elementi nemainās. Pēc tam, no visiem nākamajiem atņemot otro kolonnu, kas reizināta ar atbilstošajiem skaitļiem, visus otrās rindas elementus, izņemot otro, pagriežam uz nulli un iegūstam kanonisko matricu:
.
Apsveriet matricu A ar izmēru .
A= 
Atlasiet tajā k rindas un k kolonnas ( 
).
26. definīcija:Nepilngadīga Matricas A k-tā secība ir kvadrātmatricas determinants, ko iegūst no dotās, atlasot tajā.
k rindas un k kolonnas.
27. definīcija:rangs matrica tiek saukta par lielāko no tās nepilngadīgajām vērtībām, kas nav nulles, r(A).
28. definīcija: Tiek saukts nepilngadīgais, kura pakāpe ir tāda pati kā viņa pakāpe pamata nepilngadīgais.
Paziņojums, apgalvojums:
1. Rangs tiek izteikts kā vesels skaitlis.( 
)
2.r=0, 
kad A ir nulle.
Matricu elementārās transformācijas.
Matricu elementārās transformācijas ietver šādas:
1) jebkuras matricas rindas (kolonnas) visu elementu reizināšana ar vienu un to pašu skaitli.
2) pievienojot jebkuras matricas rindas (kolonnas) elementiem citas rindas (kolonnas) atbilstošos elementus, kas reizināti ar to pašu skaitli;
3) matricas rindu (kolonnu) permutācija;
4) nulles rindas (kolonnas) atmešana;
5) matricas rindu aizstāšana ar atbilstošām kolonnām.
29. definīcija: Matricas, kas iegūtas viena no otras elementārās pārveidojumos, sauc par ekvivalentām matricām, ko apzīmē ar “~”
Galvenā ekvivalentu matricu īpašība: Ekvivalentu matricu rindas ir vienādas.
18. piemērs: Aprēķināt r(A), 
Risinājums: Soli pa solim pirmo rindiņu reiziniet ar (-4) (-2)
(-7) un pēc tam pievienojiet attiecīgi otrajai, trešajai un ceturtajai rindai.
~
apmainīt otro un ceturto rindu 
reiziniet otro rindu ar (-2) un pievienojiet ceturtajai rindai; pievienojiet otro un trešo rindu.
pievienojiet trešo un ceturto rindu.
~
izmetiet nulles līniju
~
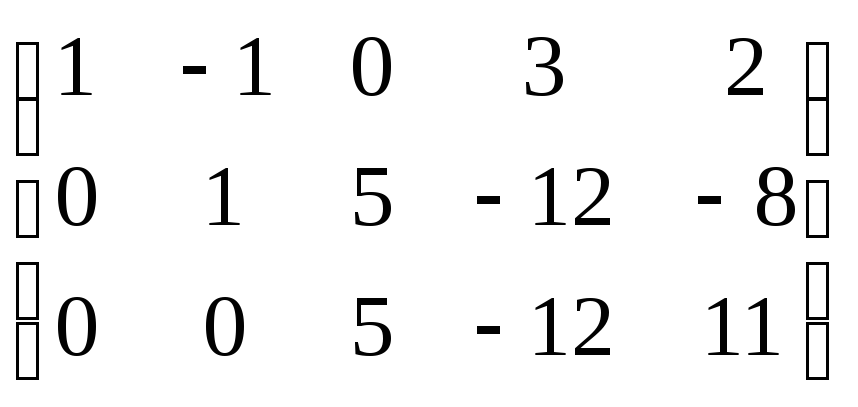r(A)=3 
rangs oriģinālā matrica
vienāds ar trīs.
30. definīcija: Matricu A saucam par soļu matricu, ja visi galvenās diagonāles elementi 
0, un elementi zem galvenās diagonāles ir nulle.
Teikums:
1) pakāpienu matricas rangs ir vienāds ar tās rindu skaitu;
2) jebkuru matricu ar elementāru pārveidojumu palīdzību var reducēt uz pakāpiena formu.
19. piemērs: Pie kādām matricas vērtībām 
vai rangs ir vienāds ar vienu?
Risinājums: Rangs ir vienāds ar vienu, ja otrās kārtas determinants ir vienāds ar nulli, t.i.
§6. Vispārīgas formas lineāro vienādojumu sistēmas.
skata sistēma 
---(9) sauc par vispārējas formas sistēmu.
31. definīcija: Divas sistēmas tiek uzskatītas par līdzvērtīgām (ekvivalentām), ja katrs pirmās sistēmas risinājums ir otrās sistēmas risinājums un otrādi.
Sistēmā (1) matrica A= 
tiks saukta par sistēmas galveno matricu, un 
=
paplašināta matricu sistēma
Teorēma. Kronecker-Cappelli
Lai sistēma (9) būtu konsekventa, ir nepieciešams un pietiekami, lai sistēmas galvenās matricas rangs būtu vienāds ar paplašinātās matricas rangu, t.i., r(A)=r( 
)
1. teorēma. Ja konsekventas sistēmas matricas rangs ir vienāds ar nezināmo skaitu, tad sistēmai ir unikāls risinājums.
2. teorēma. Ja apvienotās sistēmas matricas rangs ir mazāks par nezināmo skaitu, tad sistēmai ir bezgalīgi daudz atrisinājumu.
Noteikums patvaļīgas lineāro vienādojumu sistēmas risināšanai:
1) atrodiet sistēmas galveno un paplašināto matricu rindas. Ja 
, tad sistēma ir nekonsekventa.
2) Ja 
=r, tad sistēma ir saderīga. Atrodiet kādu pamata minora kārtas r. Mēs sauksim pamata minoru, uz kura pamata tika noteikts matricas rangs.
Nezināmie, kuru koeficienti ir iekļauti pamata minorā, tiek saukti par galvenajiem (pamata) un atstāti kreisajā pusē, bet atlikušie nezināmie tiek saukti par brīviem un pārnesti uz vienādojuma labo pusi.
3) Atrodiet galveno nezināmo izteiksmes brīvo izteiksmē. Tiek iegūts sistēmas vispārējais risinājums.
20. piemērs: Izpētiet sistēmu un tās saderības gadījumā atrodiet unikālu vai vispārīgu risinājumu 
Risinājums: 1) pēc T. Kronecker-Capelli domām, mēs atrodam sistēmas paplašināto un pamata matricu rindas:
~
~
~
~
galvenās matricas rangs ir divi
2)
atrodiet paplašinātās matricas rangu 
~
~
~
3) Secinājums:
=2, tad sistēma ir saderīga.
Bet 
sistēma ir nenoteikta, un tai ir bezgalīgs skaits risinājumu.
4) Pamata nezināmie 
un 
, jo tie pieder pie pamata nepilngadīgajiem, un 
- brīvs nezināmais.
Ļaujiet 
=c, kur c ir jebkurš skaitlis.
5) Pēdējā matrica atbilst sistēmai 
6) Atbilde: 
7) Verifikācija: jebkurā no sākotnējās sistēmas vienādojumiem, kur ir visi nezināmie, mēs aizvietojam atrastās vērtības.
Ļaujiet dot kādu matricu:
.
Izvēlieties šajā matricā 
patvaļīgas līnijas un 
patvaļīgas kolonnas 
. Tad noteicējs 
kārta, kas sastāv no matricas elementiem 
kas atrodas atlasīto rindu un kolonnu krustpunktā, tiek saukta par nepilngadīgo 
-th order matrica 
.
Definīcija 1.13. Matricas rangs 
ir šīs matricas mazākā, kas nav nulle, lielākā secība.
Lai aprēķinātu matricas rangu, jāņem vērā visi tās mazākās kārtas nepilngadīgie un, ja vismaz viens no tiem nav nulle, pāriet pie augstākās kārtas nepilngadīgajiem. Šo pieeju matricas ranga noteikšanai sauc par robežšķirtnes metodi (vai robežojošo nepilngadīgo metodi).
Uzdevums 1.4. Izmantojot nepilngadīgo robežu metodi, nosakiet matricas rangu 
.
.
Apsveriet pirmās kārtas apmales, piemēram, 
. Tad mēs pievēršamies dažu otrās kārtas robežu izskatīšanai.
Piemēram, 
.
Visbeidzot, analizēsim trešās kārtas robežu.
.
Pa šo ceļu, augstākā pakāpe ne-nulles nepilngadīgais ir 2, tātad 
.
Risinot 1.4. uzdevumu, var pamanīt, ka otrās kārtas robežojošo nepilngadīgo rinda nav nulle. Šajā sakarā rodas šāds jēdziens.
Definīcija 1.14. Matricas pamata minors ir jebkurš mazāks par nulli, kura secība ir vienāda ar matricas rangu.
Teorēma 1.2.(Pamata minora teorēma). Pamatrindas (pamata kolonnas) ir lineāri neatkarīgas.
Ņemiet vērā, ka matricas rindas (kolonnas) ir lineāri atkarīgas tad un tikai tad, ja vismaz vienu no tām var attēlot kā pārējo lineāru kombināciju.
Teorēma 1.3. Lineāri neatkarīgo matricas rindu skaits ir vienāds ar lineāri neatkarīgu matricas kolonnu skaitu un ir vienāds ar matricas rangu.
Teorēma 1.4.(Nepieciešams un pietiekams nosacījums, lai determinants būtu vienāds ar nulli). Lai noteicējs 
-tais pasūtījums 
ir vienāds ar nulli, ir nepieciešams un pietiekami, lai tā rindas (kolonnas) būtu lineāri atkarīgas.
Matricas ranga aprēķināšana, pamatojoties uz tās definīciju, ir pārāk apgrūtinoša. Tas kļūst īpaši svarīgi augstas kārtas matricām. Šajā sakarā praksē matricas rangs tiek aprēķināts, pamatojoties uz 10.2. - 10.4. teorēmu piemērošanu, kā arī matricas ekvivalences un elementāro pārveidojumu jēdzienu izmantošanu.
Definīcija 1.15. Divas matricas 
un 
tiek saukti par līdzvērtīgiem, ja to kārtas ir vienādas, t.i. 
.
Ja matricas 
un 
ir līdzvērtīgi, tad atzīmējiet 
.
Teorēma 1.5. Matricas rangs nemainās no elementārajām transformācijām.
Mēs sauksim par matricas elementārpārveidojumiem 
kādu no šīm darbībām matricā:
Rindu aizstāšana ar kolonnām un kolonnu ar atbilstošām rindām;
Matricas rindu permutācija;
Izsvītrot līniju, kuras visi elementi ir vienādi ar nulli;
Jebkuras virknes reizināšana ar skaitli, kas nav nulle;
Vienas rindas elementiem pievienojot citas rindas atbilstošos elementus, kas reizināti ar to pašu skaitli 
.
1.5. teorēmas sekas. Ja matrica 
iegūts no matricas 
izmantojot ierobežotu skaitu elementāru pārveidojumu, tad matricas 
un 
ir līdzvērtīgi.
Aprēķinot matricas rangu, tā jāsamazina līdz trapecveida formai, izmantojot ierobežotu elementāru pārveidojumu skaitu.
Definīcija 1.16. Par trapecveida nosauksim tādu matricas attēlojuma formu, kad lielākās ne-nulles kārtas robežmollā pazūd visi elementi zem diagonālajiem. Piemēram:
.
Šeit 
, matricas elementi 
pagriezt uz nulli. Tad šādas matricas attēlojuma forma būs trapecveida.
Parasti matricas tiek reducētas līdz trapecveida formai, izmantojot Gausa algoritmu. Gausa algoritma ideja ir tāda, ka, reizinot matricas pirmās rindas elementus ar atbilstošajiem faktoriem, tiek panākts, ka visi pirmās kolonnas elementi atrodas zem elementa. 
, pārvērstos uz nulli. Pēc tam, reizinot otrās kolonnas elementus ar atbilstošajiem reizinātājiem, mēs panākam, ka visi otrās kolonnas elementi atrodas zem elementa 
, pārvērstos uz nulli. Turpiniet rīkoties līdzīgi.
1.5.uzdevums. Nosakiet matricas rangu, reducējot to līdz trapecveida formai.
.
Gausa algoritma piemērošanas ērtībai varat apmainīt pirmo un trešo rindu.
.
Acīmredzot šeit 
. Taču, lai panāktu rezultātu elegantākā formā, var turpināt tālākas pārvērtības pār kolonnām.
.
Matricas rangs ir svarīgs skaitlisks raksturlielums. Tipiskākā problēma, kas prasa matricas ranga atrašanu, ir lineāro algebrisko vienādojumu sistēmas saderības pārbaude. Šajā rakstā mēs sniegsim matricas ranga jēdzienu un apsvērsim metodes tā atrašanai. Lai labāk asimilētu materiālu, mēs detalizēti analizēsim vairāku piemēru risinājumus.
Lapas navigācija.
Matricas ranga noteikšana un nepieciešamie papildu jēdzieni.
Pirms izrunāt matricas ranga definīciju, ir labi jāsaprot nepilngadīgā jēdziens, un matricas nepilngadīgo atrašana nozīmē spēju aprēķināt determinantu. Tāpēc mēs iesakām, ja nepieciešams, atgādināt raksta teoriju, matricas determinanta atrašanas metodes, determinanta īpašības.
Paņemiet matricu A secībā. Lai k ir daži dabiskais skaitlis, kas nepārsniedz mazāko no skaitļiem m un n , tas ir, 
.
Definīcija.
Neliela k-tā kārtība matrica A ir secības kvadrātmatricas determinants, kas sastāv no matricas A elementiem, kas atrodas iepriekš atlasītajās k rindās un k kolonnās, un matricas A elementu atrašanās vieta ir saglabāta.
Citiem vārdiem sakot, ja matricā A izdzēšam (p–k) rindas un (n–k) kolonnas un no atlikušajiem elementiem veidojam matricu, saglabājot matricas elementu A izkārtojumu, tad iegūtās matricas determinants ir matricas A minora k kārtas.
Apskatīsim matricas minora definīciju, izmantojot piemēru.
Apsveriet matricu 
.
Pierakstīsim vairākus šīs matricas pirmās kārtas minorus. Piemēram, ja mēs izvēlamies matricas A trešo rindu un otro kolonnu, tad mūsu izvēle atbilst pirmās kārtas minorai 
. Citiem vārdiem sakot, lai iegūtu šo minoritāti, mēs no matricas A izsvītrojām pirmo un otro rindu, kā arī pirmo, trešo un ceturto kolonnu un izveidojām determinantu no atlikušā elementa. Ja izvēlamies matricas A pirmo rindu un trešo kolonnu, tad iegūstam minoru 
.
Ilustrēsim uzskatāmo pirmās kārtas nepilngadīgo iegūšanas procedūru 
un 
.
Tādējādi matricas pirmās kārtas minori ir paši matricas elementi.
Parādīsim vairākus otrās kārtas nepilngadīgos. Atlasiet divas rindas un divas kolonnas. Piemēram, ņemiet pirmo un otro rindu un trešo un ceturto kolonnu. Ar šo izvēli mums ir otrās kārtas nepilngadīgais 
. Šo minoru var izveidot arī, dzēšot trešo rindu, pirmo un otro kolonnu no matricas A.
Vēl viena matricas A otrās kārtas minora ir .
Ilustrēsim šo otrās kārtas nepilngadīgo uzbūvi 
un 
.
Līdzīgi var atrast arī matricas A trešās kārtas nepilngadīgos. Tā kā matricā A ir tikai trīs rindas, mēs atlasām tās visas. Ja šīm rindām atlasām pirmās trīs kolonnas, tad iegūstam trešās kārtas minoru 
To var arī izveidot, izdzēšot matricas A pēdējo kolonnu.
Vēl viens trešās kārtas nepilngadīgais ir 
iegūts, izdzēšot matricas A trešo kolonnu.
Šeit ir zīmējums, kurā redzama šo trešās kārtas nepilngadīgo uzbūve 
un 
.
Dotajai matricai A nav nevienas mazākās kārtas, kas būtu augstākas par trešo, jo .
Cik matricas A kārtas k-tās kārtas nepilngadīgo pastāv?
Kārtības k nepilngadīgo skaitu var aprēķināt kā , kur 
un 
- attiecīgi kombināciju skaits no p līdz k un no n līdz k.
Kā uz n konstruēt visus k kārtas minorus matricā A no kārtas p?
Mums ir nepieciešama matricas rindu numuru kopa un kolonnu numuru kopa. Visu ierakstot p elementu kombinācijas ar k(tie atbildīs izvēlētajām matricas A rindām, konstruējot k kārtas minoru). Katrai rindu numuru kombinācijai mēs secīgi pievienojam visas n elementu kombinācijas ar k kolonnu numuriem. Šīs matricas A rindu numuru un kolonnu numuru kombināciju kopas palīdzēs sastādīt visus k kārtas minorus.
Ņemsim piemēru.
Piemērs.
Atrodiet visus matricas otrās kārtas nepilngadīgos.
Risinājums.
Tā kā sākotnējās matricas secība ir 3 reizes 3, tad kopējais otrās kārtas nepilngadīgo skaits būs 
.
Pierakstīsim visas matricas A 3 līdz 2 rindu numuru kombinācijas: 1, 2; 1, 3 un 2, 3. Visas 3 reizes 2 kolonnu numuru kombinācijas ir 1, 2; 1, 3 un 2, 3.
Paņemiet matricas A pirmo un otro rindu. Izvēloties šīm rindām pirmo un otro kolonnu, pirmo un trešo kolonnu, otro un trešo kolonnu, iegūstam attiecīgi nepilngadīgos 
Pirmajai un trešajai rindai ar līdzīgu kolonnu izvēli mums ir 
Otrajai un trešajai rindai atliek pievienot pirmo un otro, pirmo un trešo, otro un trešo kolonnu: 
Tātad tiek atrasti visi deviņi matricas A otrās kārtas nepilngadīgie.
Tagad mēs varam pāriet uz matricas ranga noteikšanu.
Definīcija.
Matricas rangs ir matricas, kas nav nulle, augstākā pakāpe.
Matricas A rangs tiek apzīmēts kā Rank(A) . Varat arī redzēt apzīmējumus Rg(A) vai Rang(A) .
No matricas ranga un matricas minora definīcijām mēs varam secināt, ka nulles matricas rangs ir vienāds ar nulli, bet nulles matricas rangs ir vismaz viens.
Matricas ranga atrašana pēc definīcijas.
Tātad, pirmā metode matricas ranga noteikšanai ir neliela uzskaites metode. Šīs metodes pamatā ir matricas ranga noteikšana.
Ļaujiet mums atrast kārtas matricas A rangu.
Īsi aprakstiet algoritmsšīs problēmas risinājums ar nepilngadīgo uzskaites metodi.
Ja ir vismaz viens matricas elements, kas nav nulle, tad matricas rangs ir vismaz vienāds ar vienu (jo ir pirmās kārtas mazais, kas nav vienāds ar nulli).
Tālāk mēs atkārtojam otrās kārtas nepilngadīgos. Ja visi otrās kārtas nepilngadīgie ir vienādi ar nulli, tad matricas rangs ir vienāds ar vienu. Ja eksistē vismaz viens otrās kārtas nepilngadīgais, kas nav nulle, tad pārejam uz trešās kārtas nepilngadīgo uzskaiti, un matricas rangs ir vismaz vienāds ar divi.
Tāpat, ja visi trešās kārtas nepilngadīgie ir nulle, tad matricas rangs ir divi. Ja ir vismaz viens trešās kārtas nepilngadīgais, kas nav nulle, tad matricas rangs ir vismaz trīs, un mēs pārejam pie ceturtās kārtas nepilngadīgo uzskaitīšanas.
Ņemiet vērā, ka matricas rangs nedrīkst pārsniegt mazāko no p un n.
Piemērs.
Atrodiet matricas rangu 
.
Risinājums.
Tā kā matrica nav nulle, tās rangs nav mazāks par vienu.
Otrās kārtas nepilngadīgais 
atšķiras no nulles, tāpēc matricas A rangs ir vismaz divi. Pārejam uz trešās kārtas nepilngadīgo uzskaiti. Visus 
lietas. 
Visi trešās kārtas nepilngadīgie ir vienādi ar nulli. Tāpēc matricas rangs ir divi.
Atbilde:
Rangs(A) = 2 .
Matricas ranga noteikšana ar nepilngadīgo fringing metodi.
Ir arī citas metodes matricas ranga atrašanai, kas ļauj iegūt rezultātu ar mazāku skaitļošanas darbu.
Viena no šīm metodēm ir fringing minor metode.
Tiksim galā ar pierobežas nepilngadīgā jēdziens.
Mēdz teikt, ka matricas A (k+1) kārtas mazais M ok apņem matricas A k kārtas minoro M, ja mazajam M ok atbilstošā matrica "satur" mazajai matricai atbilstošo matricu. M .
Citiem vārdiem sakot, matrica, kas atbilst apmales minorai M, tiek iegūta no matricas, kas atbilst robežmalai M ok, dzēšot vienas rindas un vienas kolonnas elementus.
Piemēram, apsveriet matricu 
un ņemt otrās kārtas nepilngadīgo. Pierakstīsim visus blakus esošos nepilngadīgos: 
Nepilngadīgo robežošanās metode ir pamatota ar sekojošu teorēmu (tās formulējumu piedāvājam bez pierādījumiem).
Teorēma.
Ja visi mazie, kas robežojas ar matricas A k-tās kārtas minori, kuras p ar n, ir vienādi ar nulli, tad visi matricas A mazie (k + 1) ir vienādi ar nulli.
Tādējādi, lai atrastu matricas rangu, nav nepieciešams uzskaitīt visus nepilngadīgos, kas ir pietiekami robežās. Nepilngadīgo skaitu, kas robežojas ar kārtas matricas A k-tās kārtas minoru, nosaka pēc formulas 
. Ņemiet vērā, ka nav vairāk nepilngadīgo, kas robežojas ar matricas A k-tās kārtas minoru, nekā ir (k + 1) matricas A nepilngadīgo. Tāpēc vairumā gadījumu nepilngadīgo robežošanās metodes izmantošana ir izdevīgāka nekā vienkārša visu nepilngadīgo uzskaitīšana.
Turpināsim matricas ranga atrašanu, izmantojot nepilngadīgo apmaiņu metodi. Īsi aprakstiet algoritmsšī metode.
Ja matrica A nav nulle, tad par pirmās kārtas minoru ņemam jebkuru matricas A elementu, kas atšķiras no nulles. Mēs uzskatām, ka tai robežojas nepilngadīgie. Ja tie visi ir vienādi ar nulli, tad matricas rangs ir vienāds ar vienu. Ja ir vismaz viens, kas nav nulle robežojošs nepilngadīgais (tā secība ir vienāda ar diviem), tad mēs pārejam pie tā robežas nepilngadīgo izskatīšanas. Ja tie visi ir nulle, tad Rank(A) = 2 . Ja vismaz viens blakus esošais nepilngadīgais nav nulle (tā secība ir vienāda ar trīs), tad mēs uzskatām, ka tā robežojas nepilngadīgie. utt. Rezultātā Rangs(A) = k, ja visi matricas A (k + 1) kārtas blakus esošie nepilngadīgie ir vienādi ar nulli, vai Rangs(A) = min(p, n), ja eksistē nulle. nepilngadīgais, kas robežojas ar kārtas nepilngadīgo (min( p, n) – 1) .
Izmantojot piemēru, analizēsim nepilngadīgo robežu noteikšanas metodi matricas ranga noteikšanai.
Piemērs.
Atrodiet matricas rangu 
izmantojot robežšķērsojošo nepilngadīgo metodi.
Risinājums.
Tā kā matricas A elements a 1 1 nav nulle, mēs to uzskatām par pirmās kārtas minoru. Sāksim meklēt blakus esošo nepilngadīgo, kas nav nulle: 
Tiek atrasts otrās kārtas nepilngadīgais, kas robežojas ar nulli. Uzskaitīsim tās robežās esošos nepilngadīgos (viņu 
lietas): 
Visi nepilngadīgie, kas robežojas ar otrās kārtas minoru, ir vienādi ar nulli, tāpēc matricas A rangs ir vienāds ar divi.
Atbilde:
Rangs(A) = 2 .
Piemērs.
Atrodiet matricas rangu 
ar pierobežas nepilngadīgo palīdzību.
Risinājums.
Kā pirmās kārtas minoru, kas nav nulle, mēs ņemam matricas A elementu a 1 1 = 1 . Fringing it minor no otrās kārtas 
nav vienāds ar nulli. Šis nepilngadīgais robežojas ar trešās kārtas nepilngadīgo 
. Tā kā tas nav vienāds ar nulli un tai nav robežojošā minora, matricas A rangs ir vienāds ar trīs.
Atbilde:
Rangs(A) = 3 .
Ranga atrašana, izmantojot matricas elementārās transformācijas (pēc Gausa metodes).
Apsveriet citu veidu, kā atrast matricas rangu.
Šādas matricas transformācijas sauc par elementārām:
- matricas rindu (vai kolonnu) permutācija;
- jebkuras matricas rindas (kolonnas) visu elementu reizināšana ar patvaļīgu skaitli k, kas atšķiras no nulles;
- pievienojot jebkuras rindas (kolonnas) elementiem atbilstošos citas matricas rindas (kolonnas) elementus, kas reizināti ar patvaļīgu skaitli k.
Matricu B sauc par ekvivalentu matricai A, ja B iegūts no A ar ierobežota skaita elementāru pārveidojumu palīdzību. Matricu līdzvērtību apzīmē ar simbolu "~", tas ir, tas ir rakstīts A ~ B.
Matricas ranga atrašana, izmantojot elementārās matricas transformācijas, balstās uz apgalvojumu: ja matrica B iegūta no matricas A, izmantojot ierobežotu skaitu elementāru pārveidojumu, tad Rank(A) = Rank(B) .
Šī apgalvojuma derīgums izriet no matricas determinanta īpašībām:
- Kad matricas rindas (vai kolonnas) ir permutētas, tās determinants maina zīmi. Ja tas ir vienāds ar nulli, tad, mainot rindas (kolonnas), tas paliek vienāds ar nulli.
- Reizinot visus jebkuras matricas rindas (kolonnas) elementus ar patvaļīgu skaitli k, kas atšķiras no nulles, iegūtās matricas determinants ir vienāds ar sākotnējās matricas determinantu, kas reizināts ar k. Ja sākotnējās matricas determinants ir vienāds ar nulli, tad pēc visu rindas vai kolonnas elementu reizināšanas ar skaitli k iegūtās matricas determinants arī būs vienāds ar nulli.
- Matricas noteiktas rindas (kolonnas) elementiem pievienojot atbilstošos citas matricas rindas (kolonnas) elementus, kas reizināti ar noteiktu skaitli k, tā determinants nemainās.
Elementāro pārveidojumu metodes būtība ir novest matricu, kuras rangs mums jāatrod, līdz trapecveida formai (konkrētā gadījumā līdz augšējai trīsstūrveida formai), izmantojot elementāras transformācijas.
Kam tas paredzēts? Šāda veida matricu rangu ir ļoti viegli atrast. Tas ir vienāds ar rindu skaitu, kas satur vismaz vienu elementu, kas nav nulle. Un tā kā matricas rangs elementāru transformāciju laikā nemainās, iegūtā vērtība būs sākotnējās matricas rangs.
Mēs sniedzam matricu ilustrācijas, no kurām viena jāiegūst pēc transformācijām. To forma ir atkarīga no matricas secības.
Šīs ilustrācijas ir veidnes, uz kurām mēs pārveidosim matricu A.
Aprakstīsim metodes algoritms.
Pieņemsim, ka jāatrod tādas matricas, kas nav nulle, A pakāpe (p var būt vienāda ar n).
Tātad,. Sareizināsim visus matricas A pirmās rindas elementus ar . Šajā gadījumā mēs iegūstam ekvivalentu matricu, apzīmējam to ar A (1): 
Iegūtās matricas A (1) otrās rindas elementiem pievienojam atbilstošos pirmās rindas elementus, kas reizināti ar . Trešās rindas elementiem pievienojiet atbilstošos pirmās rindas elementus, kas reizināti ar . Un tā tālāk līdz p-tajai rindai. Mēs iegūstam ekvivalentu matricu, apzīmējam to A (2) : 
Ja visi iegūtās matricas elementi, kas atrodas rindās no otrās līdz p-ajai, ir vienādi ar nulli, tad šīs matricas rangs ir vienāds ar vienu, un līdz ar to sākotnējās matricas rangs ir vienāds ar vienu.
Ja rindās no otrās līdz p-tajai ir vismaz viens elements, kas nav nulle, tad turpinām veikt transformācijas. Turklāt mēs rīkojamies tieši tāpat, bet tikai ar matricas A daļu, kas atzīmēta attēlā (2) 
Ja , tad matricas A (2) rindas un (vai) kolonnas pārkārtojam tā, lai "jaunais" elements kļūtu par nulli.
Jebkura matrica A pasūtījums m × n var aplūkot kā kolekciju m rindu vektori vai n kolonnu vektori .
rangs matricas A pasūtījums m × n sauca maksimālā summa lineāri neatkarīgi kolonnu vektori vai rindu vektori.
Ja matricas rangs A vienāds r, tad ir rakstīts:
Matricas ranga atrašana
Ļaujiet A patvaļīgas secības matrica m× n. Lai atrastu matricas rangu A piemērot tai Gausa eliminācijas metodi.
Ņemiet vērā, ja kādā izslēgšanas posmā vadošais elements izrādās vienāds ar nulli, tad doto virkni apmainām ar virkni, kurā vadošais elements atšķiras no nulles. Ja izrādās, ka tādas rindas nav, tad pārejam uz nākamo kolonnu utt.
Pēc Gausa eliminācijas kustības uz priekšu iegūstam matricu, kuras elementi zem galvenās diagonāles ir vienādi ar nulli. Turklāt var būt nulles rindu vektori.
Nenulles rindu vektoru skaits būs matricas rangs A.
Apskatīsim to visu ar vienkāršiem piemēriem.
1. piemērs
Reizinot pirmo rindu ar 4 un pievienojot otrajai rindai un reizinot pirmo rindu ar 2 un pievienojot trešajai rindai, mēs iegūstam:
Reiziniet otro rindu ar -1 un pievienojiet to trešajai rindai:
Mēs saņēmām divas rindas, kas nav nulles, un tāpēc matricas rangs ir 2.
2. piemērs
Atrodiet šādas matricas rangu:
Reiziniet pirmo rindu ar -2 un pievienojiet otrajai rindai. Līdzīgi iestatiet pirmās kolonnas trešās un ceturtās rindas elementus uz nulli:
Atiestatīsim otrās kolonnas trešās un ceturtās rindas elementus, pievienojot atbilstošās rindas otrajai rindai, kas reizināta ar skaitli -1.