Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Тема урока: Применение производной в различных областях знаний Учитель математики МБОУ «Школа № 74» Загуменнова Марина Владимировна

2 слайд

Описание слайда:

Цель урока: Узнать основные направления применения производной в разных областях науки и техники; Рассмотреть на примерах решения практических задач, как применяется производная в химии, физике, биологии, географии, экономике.

3 слайд

Описание слайда:

«Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира». Н.И. Лобачевский

4 слайд

Описание слайда:

Правила дифференцирования Производная суммы О постоянном множителе Производная произведения Производная дроби Производная сложной функции (u+v)"= u" + v‘ (Cu)"=Cu‘ (uv)"=u"v+uv‘ (u/v)"=(u"v-uv")/v2 hꞌ(x)=gꞌ(f(x))f ꞌ(x)

5 слайд

Описание слайда:

Производная в физике Задача. Движение автомобиля во время торможения описывается формулой s(t) = 30t - 5t2, (s - тормозной путь в метрах, t - время в секундах, прошедшее с начало торможения до полной остановки автомобиля). Найдите, сколько секунд автомобиль находится в движении с момента начала торможения до его полной остановки. Какое расстояние пройдет машина с начала торможения до полной ее остановки? Решение: Так как скорость есть первая производная от перемещения по времени, то v = S’(t) = 30 – 10t, т.к. при торможении скорость равна нулю, тогда 0=30–10t; 10t=30; t=3(сек). Тормозной путь S(t) = 30t - 5t2 = 30∙3-5∙32 = 90-45 = 45(м). Ответ: время торможения 3с, тормозной путь 45м.

6 слайд

Описание слайда:

Это интересно Пароход “Челюскин” в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли “Челюскин” на север и раздавили. Вот описание катастрофы: “Крепкий металл корпуса поддался не сразу, – сообщал по радио начальник экспедиции О.Ю. Шмидт. – Видно было, как льдина вдавливается в борт, и как над ней листы обшивки пучатся, изгибаясь наружу. Лед продолжал медленное, но неотразимое наступление. Вспученные железные листы обшивки корпуса разорвались по шву. С треском летели заклепки. В одно мгновение левый борт парохода был оторван от носового трюма до кормового конца палубы…” Почему произошла катастрофа?

7 слайд

Описание слайда:

Сила Р давления льда разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – α – угол наклона борта к вертикали. Q – сила трения льда о борт. Q = 0,2 R (0,2 – коэффициент трения). Если Q < F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q > F, то трение мешает скольжению льдины, и лед может смять и продавить борт. 0,2R < R tgα , tgα > 0,2; Q < F, если α > 1100. Наклон бортов корабля к вертикали под углом α > 1100 обеспечивает безопасное плавание во льдах.

8 слайд

Описание слайда:

Производная в химии Производную в химии используют для определения скорости химической реакции. Это необходимо: инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства, а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Для решения производственных задач в медицинской, сельскохозяйственной и химической промышленности просто необходимо знать скорости реакций химических веществ.

9 слайд

Описание слайда:

Задача по химии Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: р(t) = t2/2 + 3t –3 (моль). Найти скорость химической реакции через 3 секунды. Справка: Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени или производная от концентрации реагирующих веществ по времени (на языке математики концентрация была бы функцией, а время – аргументом)

10 слайд

Описание слайда:

Решение Понятие на языке химии Обозначение Понятие на языке математики Количество веществав момент времениt0 p = p(t0) Функция Интервал времени ∆t = t – t0 Приращение аргумента Изменение количества вещества ∆p = p(t0+ ∆t) – p(t0) Приращение функции Средняя скорость химической реакции ∆p/∆t Отношение приращения функции к приращению аргумента V (t) = p‘(t)

11 слайд

Описание слайда:

Производная в биологии Задача по биологии: По известной зависимости численности популяции х(t) определите относительный прирост в момент времени t. Справка: Популяция это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

12 слайд

Описание слайда:

Решение Понятие на языке биологии Обозначение Понятие на языке математики Численность в момент времениt x = x(t) Функция Интервал времени ∆t = t – t0 Приращение аргумента Изменение численности популяции ∆x = x(t) – x(t0) Приращение функции Скорость изменения численности популяции ∆x/∆t Отношение приращения функции к приращению аргумента Относительный прирост в данный момент lim∆x/∆t ∆t → 0 ПроизводнаяР = х" (t)

13 слайд

Описание слайда:

14 слайд

Описание слайда:

Производная в географии Производная помогает рассчитать: Некоторые значения в сейсмографии Особенности электромагнитного поля земли Радиоактивность ядерно- геофизичексих показателей Многие значения в экономической географии Вывести формулу для вычисления численности населения на территории в момент времени t.

15 слайд

Описание слайда:

Задача по географии Вывести формулу для вычисления численности населения на ограниченной территории в момент времени t.

16 слайд

Описание слайда:

Решение Пусть у=у(t) – численность населения. Рассмотрим прирост населения за ∆t = t – t0 ∆у = k∙y∙∆t, где k = kр – kс – коэффициент прироста населения, (kр - коэффициент рождаемости, kс – коэффициент смертности). ∆у/∆t = k∙y при ∆t → 0 получим lim ∆у/∆t = у’. Рост численности населения - у’ = k∙y. ∆t → 0 Вывод: производная в географии совмещается с многими ее отраслями(сейсмография, размещение и численность населения) а также с экономической географии. Все это позволяет полнее изучать развитие населения и стран мира.

17 слайд

Описание слайда:

Производная в экономике Производная решает важные вопросы: В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления. Также с помощью экстремума функции в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

18 слайд

Описание слайда:

Задача по экономике №1 (издержки производства) Пусть y - издержки производства, а х - количество продукции, тогда х1- прирост продукции, а у1 - приращение издержек производства.

19 слайд

Описание слайда:

20 слайд

Презентация на тему: «Применение производной в науке и в жизни» Выполнила студентка группы ПхИ-17 Долженкова Анастасия Сведения из истории появления производной: Лозунгом многих математиков XVII в. был: «Двигайтесь вперёд, и вера в правильность результатов к вам придёт». Термин «производная» - (франц. deriveе - позади, за) ввёл в 1797 г. Ж. Лагранж. Он же ввёл современные обозначения y " , f ‘. обозначение lim –сокращение латинского слова limes (межа, граница). Термин «предел» ввёл И. Ньютон. И. Ньютон называл производную флюксией, а саму функцию - флюентой. Г. Лейбниц говорил о дифференциальном отношении и обозначал производную так: Лагранж Жозеф Луи (1736-1813) французский математик и механик Ньютон:

« Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон.» А.Поуг.

Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления.

Главный его труд- «Математические начала натуральной философии»-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.

Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Что называется производной функции?

Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.

Физический смысл производной.

• Скорость есть производная от пути по времени:
v(t) = S′(t)

• Ускорение есть производная скорости по времени:

a(t) = v′(t) = S′′(t)

Геометрический смысл производной: Угловой коэффициент касательной к графику функции равен производной этой функции, вычисленной в точке касания. f′(x) = k = tga Производная в электротехнике:

В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в химии:

• И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
• Химия – это наука о веществах, о химических превращениях веществ.
• Химия изучает закономерности протекания различных реакций.
• Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.
• Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Производная в географии:

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Интеграл и его применение: Немного из истории: История понятия интеграла уходит корнями к математикам Древней Греции и Древнего Рима. Известны работы учёного Древней Греции - Евдокса Книдского (ок.408-ок.355 до н.э.) на нахождение объёмов тел и вычисления площадей плоских фигур. Большое распространение интегральное исчисление получило в XVII веке. Учёные: Г. Лейбниц (1646-1716) и И. Ньютон (1643-1727) открыли независимо друг от друга и практически одновременно формулу, названную в последствии формулой Ньютона - Лейбница, которой мы пользуемся. То, что математическую формулу вывели философ и физик никого не удивляет, ведь математика-язык, на котором говорит сама природа. Большое распространение интегральное исчисление получило в XVII веке. Учёные: Г. Лейбниц (1646-1716) и И. Ньютон (1643-1727) открыли независимо друг от друга и практически одновременно формулу, названную в последствии формулой Ньютона - Лейбница, которой мы пользуемся. То, что математическую формулу вывели философ и физик никого не удивляет, ведь математика-язык, на котором говорит сама природа. Символ введен Символ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690 г.) . Вероятно, оно происходит от латинского integero, которое переводится как приводить в прежнее состояние, восстанавливать. Пределы интегрирования указал уже Л.Эйлер (1707-1783). В 1697 году появилось название новой ветви математики - интегральное исчисление. Его ввёл Бернулли. В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как площадь, объём, масса, смещение и т. д., когда задана скорость или распределение изменений этой величины по отношению к некоторой другой величине (положение, время и т. д.). Что такое интеграл? Интеграл - одно из важнейших понятий математического анализа , которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и т. п., а также в задаче о восстановлении функции по её производной Ученые стараются все физические явления выразить в виде математической формулы. Как только у нас есть формула, дальше уже можно при помощи нее посчитать что угодно. А интеграл - это один из основных инструментов работы с функциями. Ученые стараются все физические явления выразить в виде математической формулы. Как только у нас есть формула, дальше уже можно при помощи нее посчитать что угодно. А интеграл - это один из основных инструментов работы с функциями. Методы интегрирования:

• Табличный.
• Сведение к табличному преобразованием подынтегрального выражения в сумму или разность.
• Интегрирование с помощью замены переменной (подстановкой).
• Интегрирование по частям.

Применение интеграла:

• Математика
• Вычисления S фигур.
• Длина дуги кривой.
• V тела на S параллельных сечений.
• V тела вращения и т.д

• Физика
• Работа А переменной силы.
• S – (путь) перемещения.
• Вычисление массы.
• Вычисление момента инерции линии, круга, цилиндра.
• Вычисление координаты центра тяжести.
• Количество теплоты и т.д.

Министерство образования Саратовской области

Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ

Выполнила: Саркулова Нургуля Сергеевна

студентка группы КШИ-216/15

(Конструирование, моделирование и

технология швейных изделий)

Научный руководитель:

Вербицкая Елена Вячеславовна

преподаватель математики ГАПОУ СО

«Энгельсский политехникум»

2016

Введение

Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

5. Выводы

Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y = f (x ) в точке x 0 – это скорость изменения функции f (x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y " , f " ввёл Ж.Лагранж в 1797г.

Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

y = f (x о ) + f ′(x о ) (x – x о )

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , является на этом интервале выпуклым , лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов 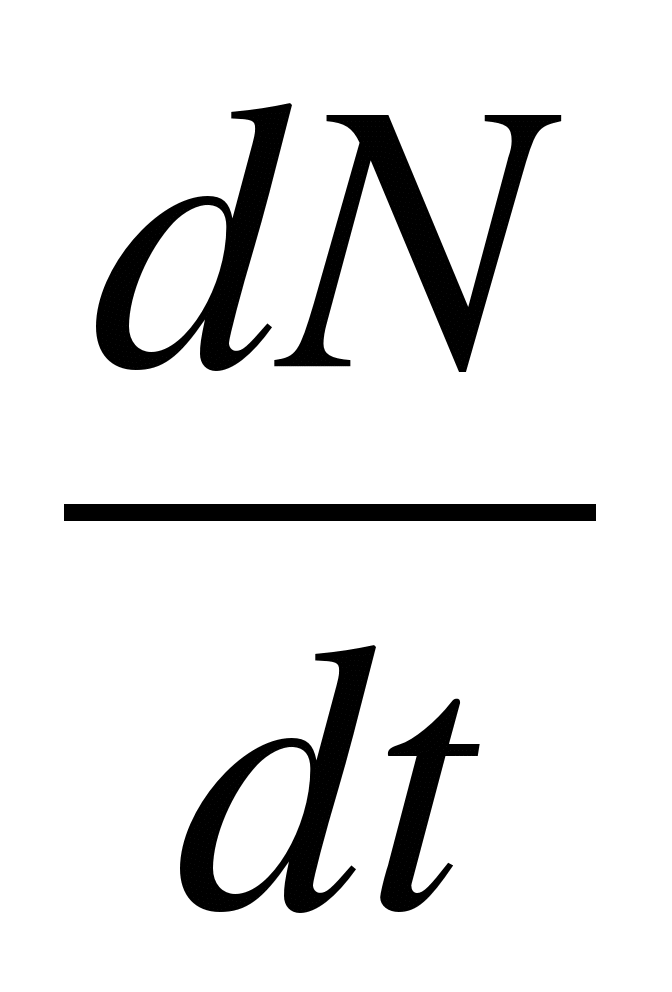= - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности . V (t) = p ‘(t)

Количество

в-ва в момент времени t 0

p = p(t 0 )

Функция

Интервал времени

∆t = t– t 0

Приращение аргумента

Изменение количества в-ва

∆p= p(t 0 + ∆ t) – p(t 0 )

Приращение функции

Средняя скорость химической реакции

∆p/∆t

Отношение приращёния функции к приращёнию аргумента

Производная в биологии:

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Р = х‘ (t)

Производная в географии:

1. Некоторые значения в сейсмографии

2. Особенности электромагнитного поля земли

3. Радиоактивность ядерно- геоифзичексих показателей

4.Многие значения в экономической географии

5.Вывести формулу для вычисления численности населения на территории в момент времени t.

у’= к у

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует

Производная в электротехнике:

В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в экономике:

Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.

Производная в экономике решает важные вопросы:

1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?

Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни

Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список используемой литературы:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.

4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.

5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.

6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.

7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010

8 . Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016

Периодические источники:

Газеты и журналы: «Математика», «Открытый урок»

Использование ресурсов сети Интернет, электронных библиотек:

www:egetutor.ru

matematika-na5.norod.ru

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока: интегрированный.

Цель урока: изучить некоторые аспекты применения производной в различных областях физики, химии, биологии.

Задачи: расширение кругозора и познавательной деятельности учащихся, развитие логического мышления и умения применять свои знания.

Техническое обеспечение: интерактивная доска; компьютер и диск.

ХОД УРОКА

I. Организационный момент

II. Постановка цели урока

– Урок хотелось бы провести под девизом Крылова Алексея Николаевича советского математика и кораблестроителя: «Теория без практики мертва или бесполезна, практика без теории невозможна или пагубна».

– Повторим основные понятия и ответим на вопросы:

– Скажите основное определение производной?
– Что вы знаете о производной (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с применением производной в физике, математике и биологии?

Рассмотрение основного определения производной и его обоснование (ответ на первый вопрос):

Производная – одно из фундаментальных понятий математики. Умение решать задачи с применением производной требует хорошего знания теоретического материала, умения проводить исследование различных ситуаций.

Поэтому сегодня на уроке мы закрепим и систематизируем полученные знания, рассмотрим и оценим работу каждой группы и на примере некоторых задач покажем, как при помощи производной решать другие задачи и нестандартные задачи с применением производной.

III. Объяснение нового материала

1. Мгновенная мощность есть производная работы по времени:

W = lim ΔA/Δt ΔA – изменение работы.

2. Если тело вращается вокруг оси, то угол поворота есть функция времени t
Тогда угловая скорость равна:

W = lim Δφ/Δt = φ׳(t) Δt → 0

3. Сила тока есть производная Ι = lim Δg/Δt = g′, где g – положительный электрический заряд переносимый через сечение проводника за время Δt.

4. Пусть ΔQ – количество теплоты, необходимое для изменения температуры за Δt времени, тогда lim ΔQ/Δt = Q′ = C – удельная теплоёмкость.

5. Задача о скорости течения химической реакции

m(t) – m(t0) – количество вещества, вступающее в реакцию от времени t0 до t

V= lim Δm/Δt = m Δt → 0

6. Пусть m – масса радиоактивного вещества. Скорость радиоактивного распада: V = lim Δm/Δt = m׳(t) Δt→0

В дифференцированной форме закон радиоактивного распада имеет вид: dN/dt = – λN, где N – число ядер не распавшихся время t.

Интегрируя это выражение, получаем: dN/N = – λdt ∫dN/N = – λ∫dt lnN = – λt + c, c = const при t = 0 числорадиоактивных ядер N = N0 , отсюда имеем: ln N0 = const, следовательно

n N = – λt + ln N0.

Потенциируя это выражение получаем:

–закон радиоактивного распада, где N0 – число ядер в момент времени t0 = 0, N – число ядер, не распавшихся за время t.

7. Согласно уравнению теплообмена Ньютона скорость потока теплоты dQ/dt прямо пропорциональна площади окна S и разности температур ΔT между внутренним и внешним стёклами и обратно пропорциональна его толщине d:

dQ/dt =A S/d ΔT

8. Явлением Диффузии называется процесс установления равновесного распределения

Внутри фаз концентрации. Диффузия идёт в сторону, выравнивая концентрации.

m = D Δc/Δx c – концентрация
m = D c׳x x – координата, D – коэффициент диффузии

Закон Фика:

9. Было известно, что электрическое поле возбуждает либо электрические заряды, либо магнитное поле, которое имеет единственный источник – электрический ток. Джеймс Кларк Максвелл ввёл одну поправку в открытые до него законы электромагнетизма: магнитное поле возникает также и при изменении электрического поля. Маленькая на первый взгляд поправка имела грандиозные последствия: появилась пусть пока и на кончике пера, совершенно новый физический объект – электромагнитная волна. Максвелл виртуозно владел, в отличии от Фарадея, которому казалось возможным её существование, вывел уравнение для электрического поля:

∂E/∂x = M∂B/Mo ∂t Mo = const t

Изменение электрического поля вызывает появление магнитного поля в любой точке пространства, другими словами, скорость изменения электрического поля определяет величину магнитного поля. Под большим электрическим током – большее магнитное поле.

IV. Закрепление изученного

– Мы с вами изучали производную и её свойства. Хотелось бы прочитать философское высказывание Гильберта: «У каждого человека есть определённый кругозор. Когда этот кругозор сужается до бесконечного малого, то он обращается в точку. Тогда человек и говорит что это и есть его точка зрения.»
Давайте попробуем измерить точку зрения на применении производной!

Сюжет «Листик» (применение производной в биологии, физике, жизни)

Рассмотрим падение как неравномерное движение зависящее от времени.

Итак: S = S(t) V = S′(t) = x′(t), a = V′(t) = S″(t)

(Теоретический опрос: механический смысл производной).

1. Решение задач

Решите самостоятельно задачи.

2. F = ma F = mV′ F = mS″

Запишем II закон Портона, и учитывая механический смысл производной перепишем его в виде: F = mV′ F = mS″

Сюжет «Волки, Суслики»

Вернёмся к уравнениям: Рассмотрим дифференциальные уравнения показательного роста и убывания: F = ma F = mV" F = mS""
Решение многих задач физики, технической биологии и социальных наук сводятся к задаче нахождения функций f"(x) = kf(x), удовлетворяющих дифференциальному уравнению, где k = const .

Формула Человека

Человек во столько раз больше атома, во сколько раз он меньше звезды:

Отсюда следует, что
Это и есть формула, определяющая место человека во вселенной. В соответствии с ней размеры человека представляют среднее пропорциональное звезды и атома.

Закончить урок хотелось бы словами Лобачевского: «Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира».

V . Решение номеров из сборника:

Самостоятельное решение задач на доске, коллективный разбор решений задач:

№ 1 Найти скорость движения материальной точки в конце 3-й секунды, если движение точки задано уравнением s = t^2 –11t + 30.

№ 2 Точка движется прямолинейно по закону s = 6t – t^2. В какой момент ее скорость окажется равной нулю?

№ 3 Два тела движутся прямолинейно: одно по закону s = t^3 – t^2 – 27t, другое - по закону s = t^2 + 1. Определить момент, когда скорости этих тел окажутся равными.

№ 4 Для машины, движущейся со скоростью 30 м/с, тормозной путь определяется формулой s(t) =30t-16t^2, где s(t) – путь в метрах, t – время торможения в секундах. В течении какого времени осуществляется торможение до полной остановки машины? Какое расстояние пройдет машина с начала торможения до полной ее остановки?

№5 Тело массой 8 кг движется прямолинейно по закону s = 2t^2+ 3t – 1. Найти кинетическую энергию тела (mv^2/2) через 3 секунды после начала движения.

Решение : Найдем скорость движения тела в любой момент времени:
V = ds / dt = 4t + 3
Вычислим скорость тела в момент времени t = 3:
V t=3 = 4 * 3 + 3=15 (м/с).
Определим кинетическую энергию тела в момент времени t = 3:
mv2/2 = 8 – 15^2 /2 = 900 (Дж).

№6 Найти кинетическую энергию тела через 4 с после начала движения, если его масса равна 25 кг, а закон движения имеет вид s = Зt^2- 1.

№7 Тело, масса которого 30 кг, движется прямолинейно по закону s = 4t^2 + t. Доказать, что движение тела происходит под действием постоянной силы.
Решение : Имеем s" = 8t + 1, s" = 8. Следовательно, a(t) = 8 (м/с^2), т. е. при данном законе движения тело движется с постоянным ускорением 8 м/с^2. Далее, так как масса тела постоянна (30 кг), то по второму закону Ньютона действующая на него сила F = ma = 30 * 8 = 240 (H) – также постоянная величина.

№8 Тело массой 3 кг движется прямолинейно по закону s(t) = t^3 – 3t^2 + 2. Найти силу, действующую на тело в момент времени t = 4с.

№9 Материальная точка движется по закону s = 2t^3 – 6t^2 + 4t. Найти ее ускорение в конце 3-й секунды.

VI . Применение производной в математике:

Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий.

Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос – на сколько зависит дальность полёта снаряда от наклона орудия – применяет её в своих трудах.

Формула производной часто встречается в работах известных математиков 17 века. Её применяют Ньютон и Лейбниц.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.

1. Построить график и исследовать функцию:

Решение данной задачи:

Минутка релаксации

VII . Применение производной в физике:

При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.

Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница.

Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).

В физике производная применяется в основном для вычисления наибольших или наименьших значений каких-либо величин.

Решение задач:

№1 Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r 2 – b/r , где a и b - положительные постоянные, r - расстояние между частицами. Найти: а) значение r0 соответствующее равновесному положению частицы; б) выяснить устойчиво ли это положение; в) Fmax значение силы притяжения; г) изобразить примерные графики зависимости U(r) и F(r) .

Решение данной задачи: Для определения r0 соответствующего равновесному положению частицы исследуем f = U(r) на экстремум.

Используя связь между потенциальной энергией поля

U и F , тогда F = – dU/dr , получим F = – dU/dr = – (2a/r3+ b/r2) = 0; при этом r = r0 ; 2a/r3 = b/r2 => r0 = 2a/b ; Устойчивое или неустойчивое равновесие определим по знаку второй производной:
d2U/dr02= dF/dr0 = – 6a/r02 + 2b/r03 = – 6a/(2a/b)4 + 2b/(2a/b)3 = (– b4/8a3) < 0 ;
равновесие устойчивое.

Для определения Fmax притяжения исследую на экстремумы функцию:F = 2a/r3 - b/r2 ;
dF/dr = –6a/r4 + 2b/ r3 = 0 ; при r = r1 = 3a/b ; подставляя, получу Fmax = 2a/r31 - b/r31 = – b3/27a2 ; U(r) = 0 ; при r = a/b ; U(r)min при r = 2, a/b = r0 ;F = 0; F(r)max при r = r1 = 3a/b ;
Ответ: F(r)max при r = r1 = 3a/b ;

№2 Цепь с внешним сопротивлением R = 0,9 Ом питается от батареи из k = 36 одинаковых источников, каждый из которых имеет ЭДС E=2 В и внутреннее сопротивление r0 = 0,4 Ом . Батарея включает n групп, соединенных параллельно, а в каждой из них содержится m последовательно соединенных аккумуляторов. При каких значениях m , n будет получена максимальная J во внешнем R.

Решение данной задачи:

При последовательном соединении аккумуляторов Eгр = m* E; rгр = r0*m ;
а при параллельном соединении одинаковых rбат = r0m/n; Eбат = m* E,
По закону Ома J = m E/(R+ r0m/n) = m En/(nR + r0m)
Т.к. k – общее число аккумуляторов, то k = mn ;
J = k E/(nR + r0m) = k E/(nR + kr0/n) ;
Для нахождения условия при котором J тока в цепи максимальная исследую функцию J = J(n) на экстремум взяв производную по n и приравняв ее к нулю.
J’n – (k E(R - kr0/n2))/ (nR + kr0/n)2 = 0;
n2 = kr/R
n = √kr/R = √3,6*0,4/0,9 = 4 ;
m = k/n = 36/4 = 9 ;
при этом Jmax = k E/(nR + mr0) = 36*2/(4*0,9 + 9*0,4) = 10 А ;

Ответ: n = 4, m = 9 .

№3 Платформа массой М начинает двигаться вправо под действием постоянной силы F . Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна µ кг/с. Пренебрегая трением, найти зависимость от времени ускорения а платформы в процессе погрузки. Определить ускорение а1 платформы в случае, если песок не насыпается на платформу, а из наполненной высыпается через отверстие в ее дне с постоянной скоростью µ кг/с.

Решение данной задачи: Рассмотрим сначала случай, когда песок насыпается на платформу
Движение системы платформа – песок можно описать с помощью второго закона Ньютона:
dP/dt = FΣ
P – импульс системы платформа – песок, FΣ – сила, действующая на систему платформа – песок.
Если через p обозначить импульс платформы, то можно написать:dp/dt = F
Найдем изменение импульса платформы за бесконечно малый промежуток времени Δt : Δp = (M + µ(t + Δt))(u + Δu) – (M + µt)u = F Δt;
где u – скорость платформы.
Раскрыв скобки и, проведя сокращения получаем:
Dp = µu Δt + M Δu+ Δµut + Δµu Δt = F Δt
Разделим на Δt и перейдем к пределу Δt → 0
Mdu/dt + µtdu/dt + µu= F или d[(M + µt)u]/dt = F
Это уравнение можно проинтегрировать, считая начальную скорость платформы равной нулю: (M + µt)u = Ft.
Следовательно: u = Ft/(M + µt)
Тогда, ускорение платформы: a = du/dt = (F(M + µt) – Ftµ)/(M + µt) 2 = FM / (M + µt) 2

Рассмотрим случай, когда песок высыпается из наполненной платформы.
Изменение импульса за малый промежуток времени:
Δp = (M – µ(t + Δt))(u+ Δu) + Δµtu – (M – µt)u = F Δt
Слагаемое Δµtu есть импульс количества песка, которое высыпалось из платформы за время Δt. Тогда:
Δp = M Δu – µt Δu – Δµt Δu = F Δt
Разделим на Δt и перейдем к пределу Δt → 0
(M – µt)du/dt = F
Или a1= du/dt= F/(M – µt)

Ответ: a = FM / (M + µt) 2 , a1= F/(M – µt)

VIII. Самостоятельная работа:

Найти производные функций:

Прямая у = 2х является касательной к функции: у = х 3 + 5х 2 + 9х + 3. Найдите абсциссу точки касания.

IX . Подведение итогов урока:

– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее сложными? Почему?

Список литературы:

1. Амелькин В.В., Садовский А.П. Математические модели и дифференциальные уравнения. – Минск: Высшая школа, 1982. – 272с.
2. Амелькин В.В. Дифференциальные уравнения в приложениях. М.: Наука. Главная редакция физико-математической литературы, 1987. – 160с.
3. Еругин Н.П. Книга для чтения по общему курсу дифференциальных уравнений. – Минск: Наука и техника, 1979. – 744с
4. .Журнал «Потенциал» Ноябрь 2007 №11
5. «Алгебра и начала анализа» 11 класс С.М. Никольский, М.К. Потапов и др.
6. «Алгебра и математический анализ» Н.Я. Виленкин и др.
7. «Математика» В.Т. Лисичкин, И.Л. Соловейчик, 1991 год

Задача. Функция издержек имеет вид , а доход при производстве х единиц товара определяется следующим образом:

Определить оптимальное для производителя значение выпуска х0.

Решение:

Прибыль Р(х) = D (x ) - С(х), где D (x ) - доход от производства х единиц продукта.

Функция прибыли имеет вид:

Найдем производную функции прибыли:

Очевидно, Р"(х)> 0 при х < 100, так что наибольшее значение прибыли на отрезке есть Р (100) = 399 900. Найдем теперь наибольшее значение прибыли на интервале (100; + ∞). Имеется одна критическая точка х= 200. При этом Р"(х) > 0 при 100 < x < 200 и Р " (х) < 0 при x > 200, т. е. х= 200- максимальное значение Р(х) на интервале (100; + ∞).

Р (200) = 419 900 > Р (100), таким образом, x опт = 200 (ед.).

Задача. Цементный завод производит Х т. цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т. цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т. в день.

Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:

К=-х3+98х2+200х . Удельные затраты составят К/х=-х2+98х+200

Решение:

Задача сводится к отысканию наибольшего и наименьшего значения функции

у= - х2+98х+200 . На промежутке .

DIV_ADBLOCK1021">

6 Применение производной в медицине

Применение дифференциального исчисления в медицине сводится к вычислению скорости. Например, скорости восстановительных реакций и скорости релаксационного процесса.

Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, изменении температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенного лекарства, его дозы. С помощью производной можно вычислить, при какой дозе лекарства реакция организма максимальна. С помощью второй производной можно определить условия, при которых скорость процесса наиболее чувствительна к каким-либо воздействиям

Задача Предположим, что х обозначает дозу назначенного лекарства, у - функция степени реакции. у=f(x)=x²(a-x), где а - некоторая положительная постоянная. При каком значении х реакция максимальна?

Решение:

https://pandia.ru/text/80/244/images/image137_6.gif" width="116" height="24">. Тогда при ..gif" width="49" height="42"> - тот уровень дозы, который дает максимальную реакцию.

Точки перегиба важны в биохимии , так как они определяют условия, при которых некоторая величина, например скорость процесса, наиболее (или наименее) чувствительна к каким-либо воздействиям.

Задача. В результате значительной потери крови содержание железа в крови уменьшилось на 210 мг. Недостаток железа вследствие его восстановления с течением времени t уменьшается по закону мг(t – сутки). Найти зависимость скорости восстановления железа в крови от времени. Вычислить эту скорость в момент t =0 и через 7 суток.

Решение:

Скорость восстановления железа:

https://pandia.ru/text/80/244/images/image144_5.gif" width="33" height="18"> скорость восстановления равна 30 мг/сутки. Через 7 суток скорость восстановления равна 11,1 мг/сут:

Релаксационный процесс – это процесс возвращения системы к состоянию устойчивого равновесия, из которого она была выведена. Во многих случаях (особенно при однократном воздействии) этот процесс описывается экспоненциальным уравнением https://pandia.ru/text/80/244/images/image147_6.gif" width="13" height="15 src="> – постоянная времени. Ее физический смысл: - это время, в течение которого начальное отклонение Научно-исследовательская деятельность" href="/text/category/nauchno_issledovatelmzskaya_deyatelmznostmz/" rel="bookmark">научно-производственной деятельности . Например, инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства , а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. В реальной жизни для решения производственных задач, в медицинской, сельскохозяйственной и химической промышленности важно знать скорости реакций химических веществ.

Пусть дана функция m=m(t), где m -количество некоторого вещества, вступившего в химическую реакцию в момент времени t . Приращению времени Δt будет соответствовать приращение Δm величины m . Отношение Δm/Δt - есть средняя скорость химической реакции за промежуток времени Δt . Предел этого отношения при стремлении Δt к нулю - есть скорость химической реакции в данный момент времени.

Задача. Зависимость между массой х вещества, получаемого в результате некоторой химической реакции и временем t выражается уравнением https://pandia.ru/text/80/244/images/image151_5.gif" width="283" height="30 src=">

Задача. Концентрация раствора изменяется с течением времени по закону: . Найти скорость растворения.

Решение:

Скорость растворение вычислим с помощью производной:

https://pandia.ru/text/80/244/images/image154_4.gif" width="139" height="42 src=">. Получите формулу для скорости роста численности популяции.

Решение:

Задача. Зависимость суточного удоя y в литрах от возраста коров х в годах определяется уравнением , где х>2 . Найдите возраст дойных коров, при котором суточный удой будет наибольшим.

Решение:

https://pandia.ru/text/80/244/images/image161_4.gif" width="77" height="23 src=">

(лет)- точка максимума, возраст дойных коров, при котором суточный удой будет наибольшим.

Заключение

В данной работе рассмотрено одно из важнейших понятий математического анализа - производная функции с точки зрения её практического применения. С помощью производной можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных возможно подробное исследование функций, более точное построение их графиков, решение уравнений и неравенств, доказательство тождеств и неравенств, нахождение наибольших и наименьших значений величин.

По всем вышеперечисленным областям применения производной подобрано и сведено в сборник около двухсот задач. Каждый раздел сборника начинается с краткого изложения теоретических основ, содержит типовые задачи с решениями и наборы упражнений для самостоятельного решения. Эти задачи расширяют кругозор и повышают интерес к производной. Они могут быть интересны и полезны студентам, увлекающимся математикой.

Литература

1. Богомолов задач по математике: учеб пособие для ссузов. – М.: Дрофа, 2005.

2. Богомолов: учеб. для ссузов / , – М.: Дрофа, 2010.

3. Богомолов. Дидактические задания: учеб. пособие для ссузов / , – М.: Дрофа, 2005.

4. Истомина: вопросы и ответы: учеб. пособие для вузов. – Ростов н/Д: Феникс, 2002.

5. Лисичкин: учеб. пособие для техникумов / , - М.:Высш. шк.,1991.

6. Никольский математического анализа: учеб. пособие для студ. ссузов.- М.: Дрофа, 2012.

7. Омельченко: учеб. пособие для ссузов. – Ростов н/Д: Феникс, 2007.

8. Филимонова: учеб. пособие для ссузов. – Ростов н/Д: Феникс, 2013.