Rango della matrice brevemente. Determinazione del rango di una matrice. Calcolo del rango di matrice per definizione. Calcolo del rango di una matrice mediante trasformazioni elementari
Consideriamo una matrice rettangolare. Se in questa matrice selezioniamo arbitrariamente K linee e K colonne, quindi gli elementi all'intersezione delle righe e delle colonne selezionate formano una matrice quadrata del k-esimo ordine. Viene chiamato il determinante di questa matrice k-esimo ordine minore matrice A. Ovviamente, la matrice A ha minori di qualsiasi ordine da 1 al più piccolo dei numeri m e n. Tra tutti i minori diversi da zero della matrice A, c'è almeno un minore il cui ordine è il più grande. Viene chiamato il più grande degli ordini diversi da zero dei minori di una data matrice rango matrici. Se il rango della matrice A è r, allora questo significa che la matrice A ha un ordine minore diverso da zero r, ma ogni minore di ordine maggiore di r, è uguale a zero. Il rango di una matrice A è indicato con r(A). È ovvio che la relazione
Calcolo del rango di una matrice usando i minori
Il rango di una matrice si trova o con il metodo di confine minore o con il metodo trasformazioni elementari. Quando si calcola il rango di una matrice nel primo modo, si dovrebbe passare da minori di ordine inferiore a minori di ordine superiore. Se è già stato trovato un D minore diverso da zero del k-esimo ordine della matrice A, allora devono essere calcolati solo i (k + 1)° ordine minori confinanti con il D minore, cioè contenendolo come minore. Se sono tutti zero, allora il rango della matrice è K.
Esempio 1Trova il rango di una matrice con il metodo dei minori confinanti
.
Soluzione.Si comincia con i minori di 1° ordine, cioè dagli elementi della matrice A. Scegliamo, ad esempio, il minore (elemento) М 1 = 1 situato nella prima riga e nella prima colonna. Confinando con l'ausilio della seconda riga e della terza colonna si ottiene la minore M 2 = , che è diversa da zero. Passiamo ora ai minori di 3° ordine, confinanti con M 2 . Ce ne sono solo due (puoi aggiungere una seconda colonna o una quarta). Li calcoliamo: 
=
0. Pertanto, tutti i minori confinanti di terzo ordine sono risultati pari a zero. Il rango della matrice A è due.
Calcolo del rango di una matrice mediante trasformazioni elementari
ElementareSi chiamano le seguenti trasformazioni matriciali:
1) permutazione di due righe (o colonne) qualsiasi,
2) moltiplicando una riga (o una colonna) per un numero diverso da zero,
3) sommando a una riga (o colonna) un'altra riga (o colonna) moltiplicata per un certo numero.
Si chiamano le due matrici equivalente, se uno di essi è ottenuto dall'altro con l'ausilio di un insieme finito di trasformazioni elementari.
Le matrici equivalenti non sono, in generale, uguali, ma i loro ranghi sono uguali. Se le matrici A e B sono equivalenti, allora si scrive come segue: A~b.
Canonicouna matrice è una matrice che ha diversi 1 di fila all'inizio della diagonale principale (il cui numero può essere zero) e tutti gli altri elementi sono uguali a zero, ad esempio,
.
Con l'aiuto di trasformazioni elementari di righe e colonne, qualsiasi matrice può essere ridotta a una canonica. Il rango di una matrice canonica è uguale al numero di quelli sulla sua diagonale principale.
Esempio 2Trova il rango di una matrice
e portarlo alla forma canonica.
Soluzione. Sottrarre la prima riga dalla seconda riga e riordinare queste righe:
.
Ora, dalla seconda e dalla terza riga, sottrai la prima, moltiplicata rispettivamente per 2 e 5:
;
sottrarre il primo dalla terza riga; otteniamo la matrice
che è equivalente alla matrice A, poiché da essa si ottiene utilizzando un insieme finito di trasformazioni elementari. Ovviamente il rango della matrice B è 2, e quindi r(A)=2. La matrice B può essere facilmente ridotta a quella canonica. Sottraendo la prima colonna, moltiplicata per opportuni numeri, da tutte quelle successive, azzeriamo tutti gli elementi della prima riga, tranne la prima, e gli elementi delle righe rimanenti non cambiano. Quindi, sottraendo la seconda colonna, moltiplicata per i numeri appropriati, da tutti quelli successivi, azzeriamo tutti gli elementi della seconda riga, tranne la seconda, e otteniamo la matrice canonica:
.
Consideriamo una matrice A di dimensione .
A= 
Seleziona k righe e k colonne al suo interno ( 
).
Definizione 26:Minore k-esimo ordine della matrice A è chiamato determinante della matrice quadrata, che si ottiene dalla selezione data in essa.
k righe e k colonne.
Definizione 27:rango matrice è chiamata il più grande degli ordini diversi da zero dei suoi minori, r(A).
Definizione 28: Viene chiamato un minore il cui ordine è uguale al suo grado minore di base.
Dichiarazione:
1. Il rango è espresso come numero intero.( 
)
2.r=0, 
quando A è zero.
Trasformazioni elementari di matrici.
Le trasformazioni elementari delle matrici includono quanto segue:
1) moltiplicazione di tutti gli elementi di qualsiasi riga (colonna) della matrice per lo stesso numero.
2) aggiunta agli elementi di qualsiasi riga (colonna) della matrice dei corrispondenti elementi di un'altra riga (colonna) moltiplicati per lo stesso numero;
3) permutazione delle righe (colonne) della matrice;
4) scartando la riga zero (colonna);
5) sostituzione di righe di matrice con colonne corrispondenti.
Definizione 29: Le matrici ottenute l'una dall'altra, sotto trasformazioni elementari, sono dette matrici equivalenti, denotate da “~“
La proprietà principale delle matrici equivalenti: I ranghi delle matrici equivalenti sono uguali.
Esempio 18: Calcola r(A), 
Soluzione: Moltiplica la prima riga passo dopo passo per (-4)(-2)
(-7) e quindi aggiungere rispettivamente alla seconda, terza e quarta riga.
~
scambiare la seconda e la quarta riga 
moltiplica la seconda riga per (-2) e aggiungi alla quarta riga; aggiungi la seconda e la terza riga.
aggiungi la terza e la quarta riga.
~
scartare la riga nulla
~
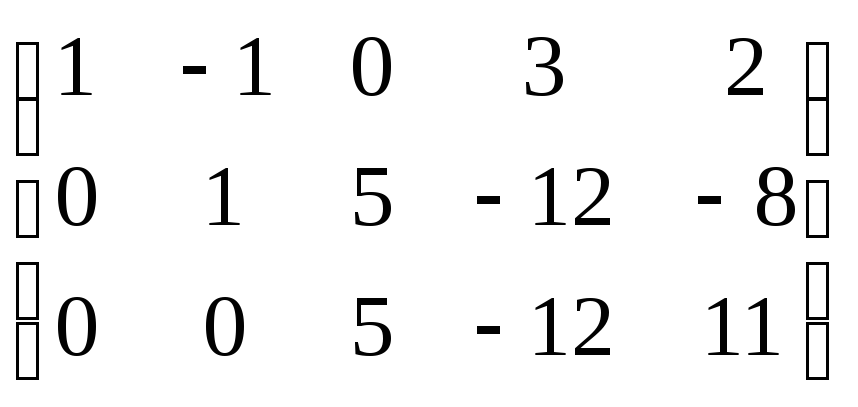r(A)=3 
rango matrice originale
è uguale a tre.
Definizione 30: Chiamiamo una matrice A matrice a gradini se tutti gli elementi della diagonale principale 
0 e gli elementi sotto la diagonale principale sono zero.
Frase:
1) il rango di una matrice di passi è uguale al numero delle sue righe;
2) qualsiasi matrice può essere ridotta a una forma a gradini con l'aiuto di trasformazioni elementari.
Esempio 19: A quali valori della matrice 
ha rango uguale a uno?
Soluzione: Il rango è uguale a uno se il determinante del secondo ordine è uguale a zero, cioè
§6. Sistemi di equazioni lineari di forma generale.
sistema di visualizzazione 
---(9) è chiamato un sistema di forma generale.
Definizione 31: Due sistemi si dicono equivalenti (equivalenti) se ogni soluzione del primo sistema è una soluzione del secondo e viceversa.
Nel sistema (1) la matrice A= 
sarà chiamata la matrice principale del sistema, e 
=
sistema a matrice espansa
Teorema. Kronecker-Cappelli
Perché il sistema (9) sia coerente, è necessario e sufficiente che il rango della matrice principale del sistema sia uguale al rango della matrice estesa, cioè r(A)=r( 
)
Teorema 1. Se il rango della matrice di un sistema articolare è uguale al numero di incognite, allora il sistema ha un'unica soluzione.
Teorema 2. Se il rango della matrice di un sistema articolare è inferiore al numero di incognite, allora il sistema ha un numero infinito di soluzioni.
La regola per risolvere un sistema arbitrario di equazioni lineari:
1) trovare i ranghi delle matrici principali ed estese del sistema. Se una 
, allora il sistema è incoerente.
2) Se 
=r, allora il sistema è coerente. Trova qualche minore di base dell'ordine r. Chiameremo il minore di base, in base al quale è stato determinato il rango della matrice.
Le incognite i cui coefficienti sono compresi nella minore di base sono dette principali (di base) e sinistre a sinistra, mentre le restanti incognite sono dette libere e trasferite a destra dell'equazione.
3) Trova le espressioni delle principali incognite in termini di quelle libere. Si ottiene la soluzione generale del sistema.
Esempio 20: Indagare il sistema e, in caso di compatibilità, trovare una soluzione unica o generale 
Soluzione: 1) secondo T. Kronecker-Capelli, troviamo i ranghi delle matrici estese e di base del sistema:
~
~
~
~
il rango della matrice principale è due
2)
trova il rango della matrice aumentata 
~
~
~
3) Conclusione:
=2, allora il sistema è coerente.
Ma 
il sistema è indefinito e ha un numero infinito di soluzioni.
4) Incognite di base 
e 
, poiché appartengono al minore di base, e 
- libero sconosciuto.
Permettere 
=c, dove c è un numero qualsiasi.
5) L'ultima matrice corrisponde al sistema 
6) Risposta: 
7) Verifica: in una qualsiasi delle equazioni del sistema originale, dove sono presenti tutte le incognite, sostituiamo i valori trovati.
Sia data qualche matrice:
.
Seleziona in questa matrice 
linee arbitrarie e 
colonne arbitrarie 
. Poi il determinante 
esimo ordine, composto da elementi di matrice 
situato all'intersezione di righe e colonne selezionate è chiamato minore 
-matrice del esimo ordine 
.
Definizione 1.13. Grado di matrice 
è l'ordine più grande del minore diverso da zero di questa matrice.
Per calcolare il rango di una matrice, si dovrebbero considerare tutti i suoi minori di ordine minimo e, se almeno uno di essi è diverso da zero, procedere alla considerazione dei minori di ordine più alto. Questo approccio alla determinazione del rango di una matrice è chiamato metodo bordering (o metodo bordering minors).
Compito 1.4. Con il metodo dei minori confinanti, determina il grado di una matrice 
.
.
Considera il confine di primo ordine, ad esempio, 
. Passiamo quindi alla considerazione di alcuni confinanti di secondo ordine.
Per esempio, 
.
Infine, analizziamo il confine del terzo ordine.
.
In questo modo, ordine più alto minore diverso da zero è 2, quindi 
.
Quando si risolve il Problema 1.4, si può notare che le serie di minori confinanti di secondo ordine sono diverse da zero. Al riguardo, si pone la seguente nozione.
Definizione 1.14. La base minore di una matrice è qualsiasi minore diverso da zero il cui ordine è uguale al rango della matrice.
Teorema 1.2.(Teorema minore di base). Le righe di base (colonne di base) sono linearmente indipendenti.
Si noti che le righe (colonne) di una matrice sono linearmente dipendenti se e solo se almeno una di esse può essere rappresentata come una combinazione lineare delle altre.
Teorema 1.3. Il numero di righe linearmente indipendenti della matrice è uguale al numero di colonne linearmente indipendenti della matrice ed è uguale al rango della matrice.
Teorema 1.4.(Condizione necessaria e sufficiente affinché il determinante sia uguale a zero). In ordine per il determinante 
-esimo ordine 
è uguale a zero, è necessario e sufficiente che le sue righe (colonne) siano linearmente dipendenti.
Calcolare il rango di una matrice in base alla sua definizione è troppo macchinoso. Questo diventa particolarmente importante per le matrici di ordine superiore. A questo proposito, in pratica, il rango di una matrice viene calcolato in base all'applicazione dei Teoremi 10.2 - 10.4, nonché all'uso dei concetti di equivalenza matriciale e trasformazioni elementari.
Definizione 1.15. Due matrici 
e 
sono detti equivalenti se i loro ranghi sono uguali, cioè 
.
Se matrici 
e 
sono equivalenti, quindi nota 
.
Teorema 1.5. Il rango di una matrice non cambia rispetto alle trasformazioni elementari.
Chiameremo trasformazioni elementari della matrice 
una delle seguenti azioni sulla matrice:
Sostituzione di righe con colonne e colonne con righe corrispondenti;
Permutazione di righe di matrice;
Cancellare una linea i cui elementi sono tutti uguali a zero;
Moltiplicando qualsiasi stringa per un numero diverso da zero;
Sommando agli elementi di una riga gli elementi corrispondenti di un'altra riga moltiplicati per lo stesso numero 
.
Corollario del Teorema 1.5. Se la matrice 
ottenuto dalla matrice 
utilizzando un numero finito di trasformazioni elementari, quindi le matrici 
e 
sono equivalenti.
Quando si calcola il rango di una matrice, dovrebbe essere ridotta a una forma trapezoidale utilizzando un numero finito di trasformazioni elementari.
Definizione 1.16. Chiameremo trapezio una tale forma di rappresentazione di una matrice, quando nel minore confinante del più grande ordine diverso da zero, tutti gli elementi al di sotto di quelli diagonali svaniscono. Per esempio:
.
Qui 
, elementi di matrice 
girare a zero. Quindi la forma di rappresentazione di tale matrice sarà trapezoidale.
Di norma, le matrici vengono ridotte a una forma trapezoidale utilizzando l'algoritmo gaussiano. L'idea dell'algoritmo gaussiano è che, moltiplicando gli elementi della prima riga della matrice per i fattori corrispondenti, ottengono che tutti gli elementi della prima colonna situati sotto l'elemento 
, verrebbe a zero. Quindi, moltiplicando gli elementi della seconda colonna per i moltiplicatori corrispondenti, otteniamo che tutti gli elementi della seconda colonna situati sotto l'elemento 
, verrebbe a zero. Procedi ulteriormente allo stesso modo.
Compito 1.5. Determina il rango di una matrice riducendola a una forma trapezoidale.
.
Per comodità di applicare l'algoritmo gaussiano, puoi scambiare la prima e la terza riga.
.
Ovviamente qui 
. Tuttavia, per portare il risultato a una forma più elegante, puoi continuare ulteriormente le trasformazioni sulle colonne.
.
Il rango di una matrice è un'importante caratteristica numerica. Il problema più caratteristico che richiede di trovare il rango di una matrice è verificare la compatibilità di un sistema di equazioni algebriche lineari. In questo articolo, daremo il concetto di rango di una matrice e considereremo i metodi per trovarlo. Per una migliore assimilazione del materiale, analizzeremo in dettaglio le soluzioni di diversi esempi.
Navigazione della pagina.
Determinazione del rango di una matrice e concetti aggiuntivi necessari.
Prima di esprimere la definizione del rango di una matrice, si dovrebbe avere una buona comprensione del concetto di minore, e trovare i minori di una matrice implica la capacità di calcolare il determinante. Quindi si consiglia, se necessario, di richiamare la teoria dell'articolo, i metodi per trovare il determinante matriciale, le proprietà del determinante.
Prendi una matrice A di ordine. Sia k alcuni numero naturale, non eccedente il più piccolo dei numeri m ed n , cioè 
.
Definizione.
Ordine k-esimo minore la matrice A è il determinante della matrice quadrata di ordine , composta dagli elementi della matrice A, che sono in k righe e k colonne preselezionate, e la posizione degli elementi della matrice A è conservata.
In altre parole, se cancelliamo (p–k) righe e (n–k) colonne nella matrice A e formiamo una matrice dagli elementi rimanenti, mantenendo la disposizione degli elementi della matrice A, allora il determinante della matrice risultante è un minore di ordine k della matrice A.
Diamo un'occhiata alla definizione di una matrice minore usando un esempio.
Considera la matrice 
.
Scriviamo diversi minori del primo ordine di questa matrice. Ad esempio, se scegliamo la terza riga e la seconda colonna della matrice A, la nostra scelta corrisponde a un minore del primo ordine 
. In altre parole, per ottenere questa minore, abbiamo cancellato dalla matrice A la prima e la seconda riga, nonché la prima, terza e quarta colonna, e dal restante elemento abbiamo costituito il determinante. Se scegliamo la prima riga e la terza colonna della matrice A, otteniamo una minore 
.
Illustriamo la procedura per ottenere i minori di primo ordine considerati 
e 
.
Pertanto, i minori del primo ordine di una matrice sono gli stessi elementi della matrice.
Mostriamo alcuni minori del secondo ordine. Seleziona due righe e due colonne. Ad esempio, prendi la prima e la seconda riga e la terza e la quarta colonna. Con questa scelta, abbiamo un minore di secondo ordine 
. Questo minore potrebbe essere formato anche cancellando la terza riga, la prima e la seconda colonna dalla matrice A.
Un altro minore di secondo ordine della matrice A è .
Illustriamo la costruzione di questi minori di secondo ordine 
e 
.
Allo stesso modo si trovano i minori di terzo ordine della matrice A. Poiché ci sono solo tre righe nella matrice A, le selezioniamo tutte. Se selezioniamo le prime tre colonne per queste righe, otteniamo una minore del terzo ordine 
Può anche essere costruito cancellando l'ultima colonna della matrice A.
Un altro minore di terzo ordine lo è 
ottenuto cancellando la terza colonna della matrice A.
Ecco un disegno che mostra la costruzione di questi minori di terzo ordine 
e 
.
Per una data matrice A non esistono minori di ordine superiore alla terza, poiché .
Quanti k-esimo ordine minori della matrice A di ordine esistono?
Il numero di ordine k minori può essere calcolato come , dove 
e 
- il numero di combinazioni da p a k e da n a k, rispettivamente.
Come costruire tutti i minori di ordine k della matrice A di ordine p su n?
Abbiamo bisogno di un insieme di numeri di riga della matrice e di un insieme di numeri di colonna. Registrazione di tutto combinazioni di p elementi per k(corrispondono alle righe selezionate della matrice A quando si costruisce un minore di ordine k). Ad ogni combinazione di numeri di riga, aggiungiamo in sequenza tutte le combinazioni di n elementi per k numeri di colonna. Questi insiemi di combinazioni di numeri di riga e di colonna della matrice A aiuteranno a comporre tutti i minori di ordine k.
Facciamo un esempio.
Esempio.
Trova tutti i minori del secondo ordine della matrice.
Soluzione.
Poiché l'ordine della matrice originale è 3 per 3, lo saranno i minori di secondo ordine totali 
.
Scriviamo tutte le combinazioni da 3 a 2 numeri di riga della matrice A: 1, 2; 1, 3 e 2, 3. Tutte le combinazioni di 3 per 2 numeri di colonna sono 1, 2 ; 1, 3 e 2, 3.
Prendi la prima e la seconda riga della matrice A. Selezionando per queste righe la prima e la seconda colonna, la prima e la terza colonna, la seconda e la terza colonna, si ottengono rispettivamente le minori 
Per la prima e la terza riga, con una scelta simile di colonne, abbiamo 
Resta da aggiungere la prima e la seconda, la prima e la terza, la seconda e la terza colonna alla seconda e alla terza riga: 
Si trovano quindi tutti e nove i minori del secondo ordine della matrice A.
Ora possiamo passare alla determinazione del rango della matrice.
Definizione.
Grado di matriceè l'ordine più alto della matrice minore diversa da zero.
Il rango della matrice A è indicato come Rank(A) . Puoi anche vedere le designazioni Rg(A) o Rang(A) .
Dalle definizioni del rango di una matrice e del minore di una matrice, possiamo concludere che il rango di una matrice zero è uguale a zero e il rango di una matrice diversa da zero è almeno uno.
Trovare il rango di una matrice per definizione.
Quindi, il primo metodo per trovare il rango di una matrice è metodo di conteggio minore. Questo metodo si basa sulla determinazione del rango della matrice.
Dobbiamo trovare il rango di una matrice A di ordine.
Descrivere brevemente algoritmo soluzione di questo problema con il metodo dell'enumerazione dei minori.
Se esiste almeno un elemento della matrice diverso da zero, il rango della matrice è almeno uguale a uno (poiché esiste un minore del primo ordine che non è uguale a zero).
Successivamente, iteriamo sui minori del secondo ordine. Se tutti i minori di secondo ordine sono uguali a zero, il rango della matrice è uguale a uno. Se esiste almeno un minore di secondo ordine diverso da zero, si passa all'enumerazione dei minori di terzo ordine e il rango della matrice è almeno uguale a due.
Allo stesso modo, se tutti i minori di terzo ordine sono zero, il rango della matrice è due. Se esiste almeno un minore di terzo ordine diverso da zero, il rango della matrice è almeno tre e si procede all'enumerazione dei minori di quarto ordine.
Si noti che il rango di una matrice non può superare il più piccolo di p e n.
Esempio.
Trova il rango di una matrice 
.
Soluzione.
Poiché la matrice è diversa da zero, il suo rango non è inferiore a uno.
Minore di secondo ordine 
è diverso da zero, quindi il rango della matrice A è almeno due. Si passa all'enumerazione dei minori di terzo ordine. Tutti loro 
le cose. 
Tutti i minori di terzo ordine sono uguali a zero. Pertanto, il rango della matrice è due.
Risposta:
Grado(A) = 2 .
Trovare il rango di una matrice con il metodo del frange minors.
Esistono altri metodi per trovare il rango di una matrice che consentono di ottenere il risultato con meno lavoro di calcolo.
Uno di questi metodi è metodo di frangitura minore.
Affrontiamo la nozione di minore confinante.
Si dice che la M ok minore del (k+1)esimo ordine della matrice A circonda la M minore di ordine k della matrice A se la matrice corrispondente alla M ok minore "contiene" la matrice corrispondente alla minore M .
In altre parole, la matrice corrispondente alla M minore bordata si ottiene dalla matrice corrispondente alla M ok minore confinante cancellando gli elementi di una riga e di una colonna.
Consideriamo ad esempio la matrice 
e prendi un minore di secondo ordine. Scriviamo tutti i minori confinanti: 
Il metodo di confinare con i minori è giustificato dal seguente teorema (ne presentiamo la formulazione senza dimostrazione).
Teorema.
Se tutti i minori confinanti con il k-esimo ordine minore di una matrice A di ordine p per n sono uguali a zero, allora tutti i minori di ordine (k + 1) della matrice A sono uguali a zero.
Quindi, per trovare il rango di una matrice, non è necessario enumerare tutti i minori sufficientemente confinanti. Il numero dei minori confinanti con il k-esimo ordine minore della matrice A dell'ordine è ricavato dalla formula 
. Si noti che non ci sono più minori confinanti con il k-esimo ordine minore della matrice A di quanti ce ne siano (k + 1)-esimo ordine minori della matrice A . Pertanto, nella maggior parte dei casi, utilizzare il metodo dei minori confinanti è più redditizio della semplice enumerazione di tutti i minori.
Procediamo a trovare il rango di una matrice con il metodo del frange minors. Descrivere brevemente algoritmo questo metodo.
Se la matrice A è diversa da zero, prendiamo qualsiasi elemento della matrice A diverso da zero come minore del primo ordine. Consideriamo i suoi minori confinanti. Se sono tutti uguali a zero, il rango della matrice è uguale a uno. Se c'è almeno un minore confinante diverso da zero (il suo ordine è pari a due), allora si passa alla considerazione dei suoi minori confinanti. Se sono tutti zero, allora Rank(A) = 2 . Se almeno un minore confinante è diverso da zero (il suo ordine è pari a tre), allora consideriamo i suoi minori confinanti. E così via. Di conseguenza, Rank(A) = k se tutti i minori confinanti del (k + 1)esimo ordine della matrice A sono uguali a zero, oppure Rank(A) = min(p, n) se esiste un diverso da zero minore confinante con un minore di ordine (min( p, n) – 1) .
Analizziamo il metodo dei minori confinanti per trovare il rango di una matrice usando un esempio.
Esempio.
Trova il rango di una matrice 
con il metodo dei minori confinanti.
Soluzione.
Poiché l'elemento a 1 1 della matrice A è diverso da zero, lo prendiamo come minore del primo ordine. Iniziamo a cercare un minore confinante diverso da zero: 
Viene trovato un minore di secondo ordine confinante diverso da zero. Elenchiamo i suoi minori confinanti (loro 
le cose): 
Tutti i minori confinanti con il minore di secondo ordine sono uguali a zero, quindi il rango della matrice A è uguale a due.
Risposta:
Grado(A) = 2 .
Esempio.
Trova il rango di una matrice 
con l'aiuto di minori confinanti.
Soluzione.
Come minore diverso da zero del primo ordine, prendiamo l'elemento a 1 1 = 1 della matrice A . Fringing minore del secondo ordine 
non è uguale a zero. Questo minore è delimitato da un minore di terzo ordine 
. Poiché non è uguale a zero e non esiste un minore confinante per esso, il rango della matrice A è uguale a tre.
Risposta:
Grado(A) = 3 .
Determinazione del rango mediante trasformazioni elementari della matrice (con il metodo di Gauss).
Considera un altro modo per trovare il rango di una matrice.
Le seguenti trasformazioni matriciali sono dette elementari:
- permutazione delle righe (o colonne) della matrice;
- moltiplicazione di tutti gli elementi di qualsiasi riga (colonna) della matrice per un numero arbitrario k diverso da zero;
- sommando agli elementi di una qualsiasi riga (colonna) gli elementi corrispondenti di un'altra riga (colonna) della matrice, moltiplicati per un numero arbitrario k.
La matrice B è chiamata equivalente alla matrice A, se B si ottiene da A con l'ausilio di un numero finito di trasformazioni elementari. L'equivalenza delle matrici è indicata dal simbolo "~", cioè si scrive A ~ B.
Trovare il rango di una matrice usando trasformazioni di matrici elementari si basa sull'affermazione: se la matrice B è ottenuta dalla matrice A usando un numero finito di trasformazioni elementari, allora Rank(A) = Rank(B) .
La validità di questa affermazione deriva dalle proprietà del determinante matriciale:
- Quando le righe (o colonne) di una matrice sono permutate, il suo determinante cambia segno. Se è uguale a zero, quando si permutano le righe (colonne), rimane uguale a zero.
- Quando si moltiplicano tutti gli elementi di qualsiasi riga (colonna) della matrice per un numero arbitrario k diverso da zero, il determinante della matrice risultante è uguale al determinante della matrice originale, moltiplicato per k. Se il determinante della matrice originale è uguale a zero, dopo aver moltiplicato tutti gli elementi di qualsiasi riga o colonna per il numero k, anche il determinante della matrice risultante sarà uguale a zero.
- Sommando agli elementi di una certa riga (colonna) della matrice gli elementi corrispondenti di un'altra riga (colonna) della matrice, moltiplicati per un certo numero k, non cambia il suo determinante.
L'essenza del metodo delle trasformazioni elementariè portare la matrice, di cui dobbiamo trovare il rango, ad un trapezio (in un caso particolare, ad un triangolare superiore) utilizzando trasformazioni elementari.
Cosa serve? Il rango di matrici di questo tipo è molto facile da trovare. È uguale al numero di righe contenenti almeno un elemento non nullo. E poiché il rango della matrice non cambia durante le trasformazioni elementari, il valore risultante sarà il rango della matrice originale.
Diamo illustrazioni di matrici, una delle quali dovrebbe essere ottenuta dopo le trasformazioni. La loro forma dipende dall'ordine della matrice.
Queste illustrazioni sono modelli in cui trasformeremo la matrice A.
Descriviamo algoritmo del metodo.
Supponiamo di dover trovare il rango di una matrice A diversa da zero di ordine (p può essere uguale a n).
Così, . Moltiplichiamo tutti gli elementi della prima riga della matrice A per . In questo caso, otteniamo una matrice equivalente, indichiamola A (1) : 
Agli elementi della seconda riga della matrice risultante A (1), aggiungiamo gli elementi corrispondenti della prima riga, moltiplicati per . Agli elementi della terza riga, aggiungi gli elementi corrispondenti della prima riga, moltiplicati per . E così via fino alla riga p-esima. Otteniamo una matrice equivalente, indichiamola A (2) : 
Se tutti gli elementi della matrice risultante nelle righe dalla seconda alla p-esima sono uguali a zero, il rango di questa matrice è uguale a uno e, di conseguenza, il rango della matrice originale è uguale a uno .
Se c'è almeno un elemento diverso da zero nelle righe dalla seconda alla p-esima, allora continuiamo ad eseguire le trasformazioni. Inoltre, agiamo esattamente allo stesso modo, ma solo con la parte della matrice A segnata in figura (2) 
Se , riorganizziamo le righe e (o) le colonne della matrice A (2) in modo che l'elemento "nuovo" diventi diverso da zero.
Qualsiasi matrice UN ordine m × n può essere visto come una raccolta m vettori di riga o n vettori di colonna.
rango matrici UN ordine m × n chiamato importo massimo vettori colonna linearmente indipendenti o vettori riga.
Se il rango della matrice UNè uguale a r, allora si scrive:
Trovare il rango di una matrice
Permettere UN matrice di ordine arbitrario m× n. Per trovare il rango di una matrice UN applica il metodo di eliminazione gaussiana ad esso.
Si noti che se a un certo punto dell'eliminazione l'elemento principale risulta essere uguale a zero, scambiamo la stringa data con la stringa in cui l'elemento principale è diverso da zero. Se risulta che non esiste una riga del genere, si passa alla colonna successiva e così via.
Dopo lo spostamento in avanti dell'eliminazione gaussiana, otteniamo una matrice i cui elementi sotto la diagonale principale sono uguali a zero. Inoltre, potrebbero esserci vettori di riga nulli.
Il numero di vettori di riga diversi da zero sarà il rango della matrice UN.
Diamo un'occhiata a tutto questo con semplici esempi.
Esempio 1
Moltiplicando la prima riga per 4 e aggiungendo alla seconda riga e moltiplicando la prima riga per 2 e sommando alla terza riga abbiamo:
Moltiplica la seconda riga per -1 e aggiungila alla terza riga:
Abbiamo due righe diverse da zero e, quindi, il rango della matrice è 2.
Esempio 2
Trova il rango della seguente matrice:
Moltiplica la prima riga per -2 e aggiungi alla seconda riga. Allo stesso modo, imposta a zero gli elementi della terza e della quarta riga della prima colonna:
Azzeriamo gli elementi della terza e quarta riga della seconda colonna sommando le righe corrispondenti alla seconda riga moltiplicate per il numero -1.